We discussed that Newtonian mechanics must be replaced by Einstein’s special theory of relativity when dealing with particle speeds comparable to the speed of light. For many other problems, however, neither relativity nor classical physics could provide agreement between theory and experiment.

A spate of discoveries right around 1900 showed that classical physics, though remarkable, was incomplete. Investigations into the nature of light and matter led to many astonishing discoveries that classical physics simply could not explain. Sometimes, as you will see, light refuses to act like a wave and seems more like a collection of particles. Other experiments found that electrons sometimes behave like waves. These discoveries eventually led to a radical new theory of light and matter called quantum physics.

Quantum mechanics was highly successful in explaining the behavior of particles of microscopic size. Like the special theory of relativity, the quantum theory requires a modification of our ideas concerning the physical world, but this article is simply an introduction to its underlying principles.

One of the most incredible discoveries of twentieth-century physics is that particles can also behave like waves and exhibit interference effects. The ability to exhibit interference effects is an essential characteristic of waves (Young's famous experiment in which light passes through two closely spaced slits and produces a pattern of bright and dark fringes on a screen, the fringe pattern is a direct indication that interference is occurring between the light waves corning from each slit). A version of Young's experiment performed by directing a beam of electrons onto a double slit, the fringe pattern indicates that the electrons are exhibiting the interference effects associated with waves. But how can electrons behave like waves in the experiment? And what kind of waves are they?. For the moment, we intend only to emphasize that the concept of an electron as a tiny discrete particle of matter does not account for the fact that the electron can behave as a wave in some circumstances. In other words, the electron exhibits a dual nature, with both particle-like characteristics and wave-like characteristics.

Here is another interesting question: If a particle can exhibit wave-like properties, can waves exhibit particle-like behavior? As the next three sections reveal, the answer is yes. In fact, experiments that demonstrated the particle-like behavior of waves were performed near the beginning of the twentieth century, before the experiments that: demonstrated the wave-like properties of the electrons. Scientists now accept the wave-particle duality as an essential part of nature.

It’s time to putter around in your garage again and try to get your mind off the constant physics questions that arise from your daily observations. You decide to clean up a box of old equipment in a corner and throw away things for which you can see no need. While going through the equipment, you come upon something you didn’t realize was there: an old variable transformer. You can plug an electrical device into its output and then dial in whatever AC voltage you want to apply to it: 0–120 volts! You grab an old lamp, plug it into the transformer and screw an incandescent light bulb into the lamp. You set the transformer at its highest voltage and turn it on. The lamp lights. Now you slowly turn the transformer voltage down. The bulb stays lit, almost all the way down to zero volts. As the voltage drops, the light from the filament gets dimmer, but it also changes color! At high voltages, the light is yellow-white, but it becomes more orange as the voltage drops, Why does that happen?

All bodies, no matter how hot or cold, continuously radiate electromagnetic waves. For instance, we see the glow of very hot objects because they emit electromagnetic waves in the visible region of the spectrum. Our sun, which has a surface temperature of about 6000 K, appears yellow, while the cooler star Betelgeuse has a red-orange appearance due to its lower surface temperature of 2900 K. However, at relatively low temperatures, cooler objects emit visible light waves only weakly and, as a result, do not appear to be glowing. Certainly the human body, at only 310 K, does not emit enough visible light to be seen in the dark with the unaided eye. But the body does emit electromagnetic waves in the infrared region of the spectrum, and these can be detected with infrared-sensitive devices.

At a given temperature, the intensities of the electromagnetic waves emitted by an object vary from wavelength to wavelength throughout the visible, infrared, and other regions of the spectrum.

Planck’s Hypothesis (Energy is quantized)

In 1900 Planck calculated the blackbody radiation curves, using a model that represents a blackbody as a large number of atomic oscillators, each of which emits and absorbs electromagnetic waves. To obtain agreement between the theoretical and experimental curves, Planck assumed that the energy E of an atomic oscillator could have only the discrete values of E = 0, hf, 2hf, 3hf, and so on. In other words, he assumed that:

$$E=nhf \;\;\;\;\;\;\;\; n=0,1,2,3,..$$

where n is either zero or a positive integer, f is the frequency of vilbration (in hertz), and h is a constant now called Planck's constant.

It is now known that the energy of a harmonic oscillator is $E = (n + \frac{1}{2})hf$; the extra term of $\frac{1}{2}$ is unimportant to the present discussion.

Blackbody radiation was the first phenomenon to be explained with a quantum model. In the latter part of the 19th century, at the same time that data were taken on thermal radiation, experiments showed that light incident on certain metallic surfaces causes electrons to be emitted from those surfaces. This phenomenon is known as the photoelectric effect, and the emitted electrons are called photoelectrons.

Einstein's photoelectric theory (Light is a collection of photons)

In 1905 Einstein presented an explanation of the photoelectric effect that took advantage of Planck's work concerning blackbody radiation. Einstein proposed that light of frequency f could be regarded as a collection of discrete packets of energy (photons), each packet containing an amount of energy E given by:

$$E_{photon} = hf$$

where h is Planck's constant. The light energy given off by a light bulb, for instance, is carried by photons. The brighter the bulb, the greater is the number of photons emitted per second.

Although Einstein presented his photon model for the photoelectric effect in 1905, it was not until 1923 that the photon concept began to achieve widespread acceptance. It was then that the American physicist Arthur H. Compton ( 1892-1962) used the photon model to explain his research on the scattering of X-rays by the electrons in graphite. X-rays are high-frequency electromagnetic waves and, like light, they are composed of photons.

The Momentum of a Photon

For an initially stationary electron, conservation of total linear momentum requires that:

Momentum of incident photon = Momentum of scattered photon + Momentum of recoil electron

A photon travels at the speed of light, so that we have v = c, and the momentum of a photon is:

$$p= \dfrac{E}{c}=\dfrac{h}{\lambda} $$

This result only applies to a photon and does not apply to a particle with mass, because such a particle cannot travel at the speed of light.

As a graduate student in 1923, Louis de Broglie (1892-1987) made the astounding suggestion that since light waves could exhibit particle-like behavior, particles of matter should exhibit wave-like behavior. De Broglie proposed that all moving matter has a wavelength associated with it, just as a wave does. He made the explicit proposal that the wavelength $\lambda$ of a particle is given by the same relation that applies to a photon:

$$\lambda= \dfrac{h}{p}$$

The wave function of a particle

 

 

The de Broglie equation for particle wavelength provides no hint as to what kind of wave is associated with a particle of matter. To gain some insight into the nature of this wave, we turn our attention to the above Figure. Part a shows the fringe pattern on the screen when electrons are used in a version of Young's double-slit experiment. The bright fringes occur in places where particle waves coming from each slit interfere constructively, while the dark fringes occur in places where the waves interfere destructively.

When an electron passes through the double-slit arrangement and strikes a spot on the screen, the screen glows at that spot, and parts b, c, and d of the above Figure illustrate how the spots accumulate in time. As more and more electrons strike the screen, the spots eventually form the fringe pattern that is evident in part d. Bright fringes occur where there is a high probability of electrons striking the screen, and dark fringes occur where there is a low probability. Here lies the key to understanding particle waves. Particle waves are waves of probability, waves whose magnitude at a point in space gives an indication of the probability that the particle will be found at that point. At the place where the screen is located, the pattern of probabilities conveyed by the particle waves causes the fringe pattern to emerge. The fact that no fringe pattern is apparent in part b of the figure does not mean that there are no probability waves present; it just means that too few electrons have struck the screen for the pattern to be recognizable.

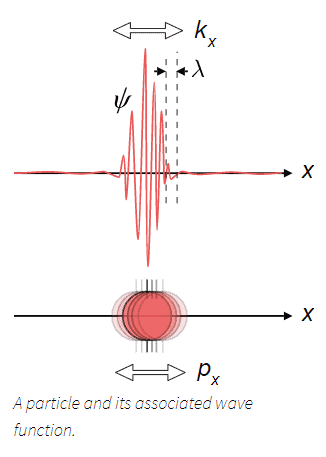
The pattern of probabilities that leads to the fringes in the above Figure is analogous to the pattern of light intensities that is responsible for the fringes in Young's original experiment with light waves. We discusses the fact that the intensity of the light is proportional to either the square of the electric field strength or the square of the magnetic field strength of the wave. In an analogous fashion in the case of particle waves, the probability is proportional to the square of the magnitude $\psi$ (Greek letter psi) of the wave. $\psi$ is referred to as the wave function of the particle.

Schrodinger equation

In 1925 the Austrian physicist Erwin Schrodinger (1887-1961) and the German physicist Werner Heisenberg (1901-1976) independently developed theoretical frameworks for determining the wave function. In so doing, they established a new branch of physics called quantum mechanics. The word "quantum" refers to the fact that in the world of the atom, where particle waves must be considered, the particle energy is quantized, so only certain energies are allowed.

To understand the structure of the atom and the phenomena related to it, quantum mechanics is essential, and the Schrodinger equation for calculating the wave function is now widely used.

The Heisenberg Uncertainty Principle

As we saw, the bright fringes in the above indicate the places where there is a high probability of an electron striking the screen. Since there are a number of bright fringes, there is more than one place where each electron has some probability of hitting. As a result, it is not possible to specify in advance exactly where on the screen an individual electron will hit. All we can do is speak of the probability that the electron may end up in a number of different places. No longer is it possible to say, as Newton's laws would suggest, that a single electron, fired through the double slit, will travel directly forward in a straight line and strike the screen. This simple model just does not apply when a particle as small as an electron passes through a pair of closely spaced narrow slits. Because the wave nature of particles is important in such circumstances, we lose the ability to predict with 100% certainty the path that a single particle will follow. Instead, only the average behavior of large numbers of particles is predictable, and the behavior of any individual particle is uncertain.

It was Heisenberg who first suggested that the uncertainty in the y component of the momentum is related to the uncertainty in the y position of the electron as the electron passes through the slit:

THE HEISENBERG UNCERTAINTY PRINCIPLE

Momentum and position: $(\Delta p_y)(\Delta y) \geq \dfrac{h}{4 \pi}$

$\Delta y$ = uncertainty in a particle's position along the y direction

$\Delta p_y$ = uncertainty in the y component of the linear momentum of the particle

 

Energy and time: $(\Delta E)(\Delta t) \geq \dfrac{h}{4 \pi}$

$\Delta E$ = uncertainty in the energy of a particle when the particle is in a certain state

$\Delta t$ = time interval during which the particle is in the state

 

The Heisenberg uncertainty principle places limits on the accuracy with which the momentum and position of a particle can be specified simultaneously. These limits are not just limits due to faulty measuring techniques. They are fundamental limits imposed by nature, and there is no way to circumvent them. First Equation indicates that $\Delta p_y$ and $\Delta y$ cannot both be arbitrarily small at the same time. If one is small, then the other must be large, so that their product equals or exceeds Planck's constant divided by $4 \pi$. For example, if the position of a particle is known exactly, so that $\Delta y$ is zero, then $\Delta p_y$ is an infinitely large number, and the momentum of the particle is completely uncertain. Conversely, if we assume that $\Delta p_y$ is zero, then $\Delta y$ is an infinitely large number, and the position of the particle is completely uncertain. In other words, the Heisenberg uncertainty principle states that it is impossible to specify precisely both the momentum and position of a particle at the same time.

There is also an uncertainty principle that deals with energy and time, as expressed by the second Equation. The product of the uncertainty $\Delta E$ in the energy of a particle and the time interval $\Delta t$ during which the particle remains in a given energy state is greater than or equal to Planck's constant divided by $4 \pi$. Therefore, the shorter the lifetime of a particle in a given state, the greater is the uncertainty in the energy of that state.

The uncertainty principle has significant consequences for the motion of tiny particles such as electrons but has little effect on the motion of macroscopic objects, even those with as little mass as a Ping-Pong ball.