We have discussed how motion is described in terms of velocity and acceleration. Now we deal with the question of why objects move as they do: What makes an object at rest begin to move? What causes an object to accelerate or decelerate? What is involved when an object moves in a curved path? We can answer in each case that a force is required. Here, we will investigate the connection between force and motion, which is the subject called dynamics.

Imagine that a train is speeding down a railroad track at 80 km/h when suddenly the engineer sees a truck stalled at a railroad crossing ahead. The engineer applies the brakes to try to stop the train before it crashes into the truck. Because the brakes cause an acceleration in the direction opposite the train’s velocity, the train will slow down. Imagine that, in this case, the engineer is able to stop the train just before it crashes into the truck. But what if instead of moving at 80 km/h the train had been moving at 100 km/h? What would have to happen for the train to avoid hitting the truck? The acceleration provided by the train’s brakes would have to be greater because the engineer still has the same distance in which to stop the train. Similarly, if the train was going 80 km/h but had been much closer to the truck when the engineer started to apply the brake, the acceleration also would need to be greater because the train would need to stop in less time.

What happened to make the train slow down? A force is a push or pull exerted on an object.

Intuitively, we experience force as any kind of a push or a pull on an object. When you push a stalled car or a grocery cart, you are exerting a force on it. When a motor lifts an elevator, or a hammer hits a nail, or the wind blows the leaves of a tree, a force is being exerted. We often call these contact forces because the force is exerted when one object comes in contact with another object. On the other hand, we say that an apple falls because of the force of gravity which is not a contact force as the earth exerts this force even when it is not in direct contact with the apple. Such forces are referred to as noncontact forces or action-at-a-distance forces, in which two objects exert forces on one another even though they are not touching.

Forces can cause objects to speed up, slow down, or change direction as they move. If an object is at rest, to start it moving requires force—that is, a force is needed to accelerate an object from zero velocity to a nonzero velocity. For an object already moving, if you want to change its velocity—either in direction or in magnitude—a force is required. In other words, to accelerate an object, a force is always required. Based on the definitions of velocity and acceleration, this can be restated as follows: a force exerted on an object causes that object’s velocity to change; that is, a force causes an acceleration.

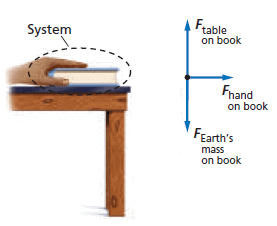When considering how a force affects motion, it is important to identify the object of interest. This object is called the system. Everything around the object that exerts forces on it is called the external world. Arrows are used to represent the forces. It is appropriate to use arrows, because a force is a vector quantity and has both a magnitude and a direction. The direction of the arrow gives the direction of the force, and the length is proportional to its strength or magnitude.

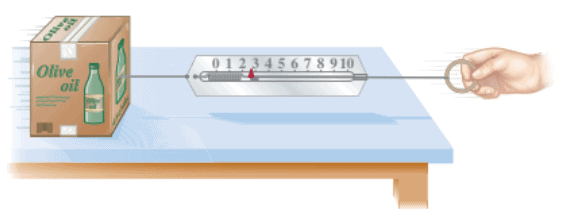One way to measure the magnitude (or strength) of a force is to use a spring scale. The spring scale, once calibrated, can be used to measure some kinds of forces, such as the pulling force shown in the Figure:

The word mass is just as familiar as the word force. A massive supertanker, for instance, is one that contains an enormous amount of mass. As we will see in the next section, it is difficult to set such a massive object into motion and difficult to bring it to a halt once it is moving. In comparison, a penny does not contain much mass. The emphasis here is on the amount of mass, and the idea of direction is of no concern. Therefore, mass is a scalar quantity.

 

During the seventeenth century, Isaac Newton, building on the work of Galileo, developed three important laws that deal with force and mass. Collectively they are called "Newton's laws of motion" and provide the basis for understanding the effect that forces have on an object.

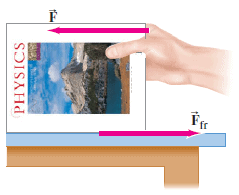To push an object with a rough surface along a tabletop at constant speed requires a certain amount of force. To push an equally heavy object with a very smooth surface across the table at the same speed will require less force. If a layer of oil or other lubricant is placed between the surface of the object and the table, then almost no force is required to keep the object moving. Notice that in each successive step, less force is required. As the next step, we imagine there is no friction at all, that the object does not rub against the table—or there is a perfect lubricant between the object and the table—and theorize that once started, the object would move across the table at constant speed with no force applied. A steel ball bearing rolling on a hard horizontal surface approaches this situation. So does a puck on an air table, in which a thin layer of air reduces friction almost to zero.

Think about the game of ice hockey. If a player does not hit a stationary puck, it will remain at rest on the ice. After the puck is struck, however, it coasts on its own across the ice, slowing down only slightly because of friction. Since ice is very slippery, there is only a relatively small amount of friction to slow down the puck. In fact, if it were possible to remove all friction and wind resistance, and if the rink were infinitely large, the puck would coast forever in a straight line at a constant speed. Left on its own, the puck would lose none of the velocity imparted to it at the time it was struck.

This is the essence of Newton's first law of motion:

Every object continues in its state of rest, or of uniform velocity in a straight line, as long as no net force acts on it.

In the first law the phrase "net force" is crucial. Often, several forces act simultaneously on a body, and the net force is the vector sum of all of them. Individual forces matter only to the extent that they contribute to the total. For instance, if friction and other opposing forces were absent, a car could travel forever at 30 mis in a straight line, without using any gas after it had come up to speed. In reality gas is needed, but only so that the engine can produce the necessary force to cancel opposing forces such as friction. This cancellation ensures that there is no net force to change the state of motion of the car.

When an object moves at a constant speed in a constant direction, its velocity is constant. Newton's first law indicates that a state of rest (zero velocity) and a state of constant velocity are completely equivalent, in the sense that neither one requires the application of a net force to sustain it. The purpose served when a net force acts on an object is not to sustain the object's velocity, but, rather, to change it.

The tendency of an object to maintain its state of rest or of uniform velocity in a straight line is called inertia. As a result, Newton’s first law is often called the law of inertia.

Inertia and Mass

A greater net force is required to change the velocity of some objects than of others. For instance, a net force that is just enough to cause a bicycle to pick up speed will cause only an imperceptible change in the motion of a freight train. In comparison to the bicycle, the train has a much greater tendency to remain at rest. Accordingly, we say that the train has more inertia than the bicycle.

Quantitatively, the inertia of an object is measured by its mass. The following definition of inertia and mass indicates why Newton's first law is sometimes called the law of inertia:

Inertia is the natural tendency of an object to remain at rest or in motion at a constant velocity. The mass of an object is a quantitative measure of inertia.

An Inertial Reference Frame

Newton’s first law does not hold in every reference frame as it can appear to be invalid to certain observers. For example, if you are a passenger riding in an accelerating car (your reference frame is an accelerating car), an object such as a cup resting on the dashboard may begin to move toward you (it stayed at rest as long as the car’s velocity remained constant). The cup accelerated toward you, but neither you nor anything else exerted a force on it in that direction.

The first law leads you to believe that the cup and you and the car motion should change relative to the ground outside. But relative to the car, you can see that your motion does not change, because you remain stationary with respect to the car.

Similarly, in the reference frame of the decelerating bus, in Example school bus comes to a sudden stop, and all of the backpacks on the floor start to slide forward, there was no force pushing the backpacks forward.

Clearly, Newton's first law does not hold for observers who use the accelerating car as a frame of reference. As a result, such a reference frame is said to be noninertial. All accelerating reference frames are noninertial.

In contrast, observers for whom the law of inertia is valid are said to be using inertial reference frames for their observations, An inertial reference frame is one in which Newton's law of inertia is valid.

The acceleration of an inertial reference frame is zero, so it moves with a constant velocity. All of Newton's laws of motion are valid in inertial reference frames, and when we apply these laws, we will be assuming such a reference frame. For most purposes, we usually make the approximation that a reference frame fixed on the Earth is an inertial frame. This is not precisely true, due to the Earth’s rotation, but usually it is close enough.

Newton's first law indicates that if no net force acts on an object, then the velocity of the object remains unchanged. The second law deals with what happens when a net force does act.

A net force exerted on an object may make its velocity increase. Or, if the net force is in a direction opposite to the motion, that force will reduce the object’s velocity. If the net force acts sideways on a moving object, the direction of the object’s velocity changes. That change in the direction of the velocity is also an acceleration. So a sideways net force on an object also causes acceleration. In general, we can say that a net force causes acceleration. Consider a hockey puck. When a player strikes a stationary puck, he causes the velocity of the puck to change. In other words, he makes the puck accelerate. The cause of the acceleration is the force that the hockey stick applies. As long as this force acts, the vellocity increases, and the puck accelerates. Now, suppose another player strikes the puck and applies twice as much force as the first player does. The greater force produces a greater acceleration. In fact, if the friction between the puck and the ice is negligible, and if there is no wind resistance, the acceleration of the puck is directly proportional to the force. Twice the force produces twice the acceleration. Moreover, the acceleration is a vector quantity, just as the force is, and points in the same direction as the force. Often, several forces act on an object simultaneously. Friction and wind resistance, for instance, do have some effect on a hockey puck. In such cases, it is the net force, or the vector sum of all the forces acting, that is important. Newton's second law states that the acceleration is proportional to the net force acting on the object.

In Newton's second law, the net force is only one of two factors that determine the acceleration. The other is the inertia or mass of the object. After all, the same net force that imparts an appreciable acceleration to a hockey puck (small mass) will impart very little acceleration to a semitrailer truck (large mass). Newton's second law states that for a given net force, the magnitude of the acceleration is inversely proportional to the mass. Twice the mass means one-half the acceleration, if the same net force acts on both objects. Thus, the second law shows how the acceleration depends on both the net force and the mass.

These relationships are found to hold in general and can be summarized as follows:

The acceleration of an object is directly proportional to the net force acting on it, and is inversely proportional to the object’s mass. The direction of the acceleration is in the direction of the net force acting on the object. This is Newton’s second law of motion.

Newton’s second law can be written as an equation:

$$\vec{a}=\dfrac{\sum \vec{F}}{m}$$ $$\sum \vec{F}= m \vec{a}$$

According to Equation, the SI unit for force is the unit for mass (kg) times the unit for acceleration (m/s$^2$) , or: $\left( \dfrac{kg . m}{s^2} \right)$ this combination is called a newton (N) and is a derived SI unit, not a base unit; 1 newton= 1 N = 1 kg· m/s$^2$ .

Every force is a vector, with magnitude and direction. Newton's second law is a vector equation valid in any inertial reference frame. It can be written in component form in rectangular coordinates as:

$$ \sum \vec{F_x}= m \vec{a_x} \;\;\;\;\;\;\;\;\;\; \sum \vec{F_y}= m \vec{a_y} \;\;\;\;\;\;\;\;\;\; \sum \vec{F_z}= m \vec{a_z}$$

If the motion is all along a line (one-dimensional), we can leave out the subscripts $\sum \vec{F}= m \vec{a}$. Sometimes the net force $\sum \vec{F}$ is written as $\vec{F_{net}}$.

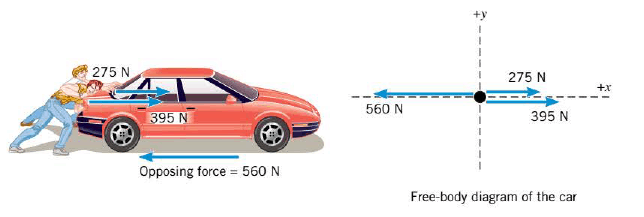When using the second law to calculate the acceleration, it is necessary to determine the net force that acts on the object. In this determination a free-body diagram helps enormously. A freebody diagram is a diagram that represents the object and the forces that act on it. Only the forces that act on the object appear in a free-body diagram. Forces that the object exerts on its environment are not included.

Newton’s second law, like the first law, is valid only in inertial reference frames. In the noninertial reference frame of a car that begins accelerating, a cup on the dashboard starts sliding—it accelerates—even though the net force on it is zero. Thus $\sum \vec{F}= m \vec{a}$ does not work in such an accelerating reference frame ($\sum \vec{F}=0$ but $\vec{a} \neq 0 $ in this noninertial frame).

 

Newton’s second law of motion describes quantitatively how forces affect motion. But where, we may ask, do forces come from? Observations suggest that a force exerted on any object is always exerted by another object. A horse pulls a wagon, a person pushes a grocery cart, a hammer pushes on a nail, a magnet attracts a paper clip. In each of these examples, a force is exerted on one object, and that force is exerted by another object. For example, the force exerted on the nail is exerted by the hammer. But things are not so one-sided. True, the hammer exerts a force on the nail. But the nail evidently exerts a force back on the hammer as well, the latter force decelerates the hammer and brings it to rest upon contact (the hammer’s speed is rapidly reduced to zero).

Only a strong force could cause such a rapid deceleration of the hammer. Thus, said Newton, the two objects must be treated on an equal basis. The hammer exerts a force on the nail, and the nail exerts a force back on the hammer. This is the essence of Newton’s third law of motion: Whenever one object exerts a force on a second object, the second object exerts an equal force in the opposite direction on the first.

Imagine you are in a football game. You line up facing your opponent, the ball is snapped, and the two of you crash together. No doubt, you feel a force. But think about your opponent. He too feels something, for while he is applying a force to you, you are applying a force to him. In other words, there isn't just one force on the line of scrimmage; there is a pair of forces. Newton was the first to realize that all forces occur in pairs and there is no such thing as an isolated force, existing all by itself. His third law of motion deals with this fundamental characteristic of forces.

The third law is often called the "action-reaction" law, because it is sometimes quoted as follows: "For every action (force) there is an equal, but opposite, reaction". But to avoid confusion, it is very important to remember that the “action” force and the “reaction” force are acting on different objects.

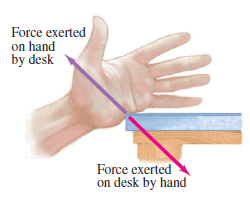As evidence for the validity of Newton’s third law, look at your hand when you push against the edge of a desk. Your hand’s shape is distorted, clear evidence that a force is being exerted on it. You can see the edge of the desk pressing into your hand. You can even feel the desk exerting a force on your hand; it hurts! The harder you push against the desk, the harder the desk pushes back on your hand. (You only feel forces exerted on you; when you exert a force on another object, what you feel is that object pushing back on you). The force the desk exerts on your hand has the same magnitude as the force your hand exerts on the desk. This is true not only if the desk is at rest but is true even if the desk is accelerating due to the force your hand exerts.

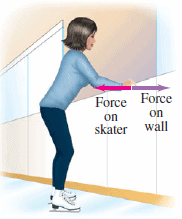As another demonstration of Newton’s third law, consider the ice skater in the Figure. There is very little friction between her skates and the ice, so she will move freely if a force is exerted on her. She pushes against the wall; and then she starts moving backward. The force she exerts on the wall cannot make her start moving, because that force acts on the wall. Something had to exert a force on her to start her moving, and that force could only have been exerted by the wall. The force with which the wall pushes on her is, by Newton’s third law, equal and opposite to the force she exerts on the wall.

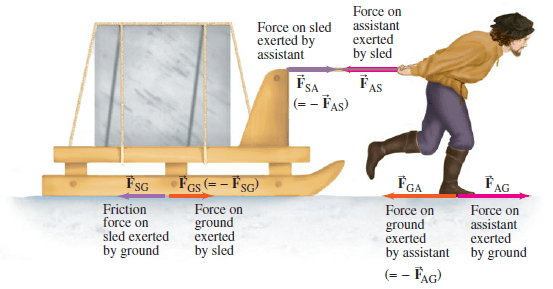In the Figure, The action and the reaction forces have the same magnitude (Newton’s third law), and the minus sign reminds us that these two forces are in opposite directions. Note carefully that the two forces shown in the Figure act on different objects—to emphasize this we used slightly different colors for the vector arrows representing these forces. These two forces would never appear together in a sum of forces in Newton’s second law, $\sum \vec{F}= m \vec{a}$. Why not? Because they act on different objects: $\vec{a}$ is the acceleration of one particular object, and $\sum \vec{F}$ must include only the forces on that one object.

Newton's three laws of motion make it clear that forces play a central role in determining the motion of an object. Now, some common forces will be discussed. It is important to realize that Newton's second law is always valid, regardless of which of these forces may act on an object. One does not have a different law for every type of common force. Thus, we need only to determine what forces are acting on an object, add them together to form the net force, and then use Newton's second law to determine the object's acceleration.

In nature there are two general types of forces, fundamental and nonfundamental. Fundamental forces are the ones that are truly unique, in the sense that all other forces can be explained in terms of them. Only three fundamental forces have been discovered: Gravitational force, Strong nuclear force, Electroweak force.

Except for the gravitational force, all of the forces discussed here are nonfundamental, because they are related to the electromagnetic force. They arise from the interactions between the electrically charged particles that comprise atoms and molecules. Our understanding of which forces are fundamental, however, is continually evolving. For instance, in the 1860s and 1870s James Clerk Maxwell showed that the electric force and the magnetic force could be explained as manifestations of a single electromagnetic force. Then, in the 1970s, Sheldon Glashow (1932- ), Abdus Salam (1926-1996), and Steven Weinberg (1933-) presented the theory that explains how the electromagnetic force and the weak nuclear force are related to the electroweak force. They received a Nobel Prize in 1979 for their achievement. Today, efforts continue that have the goal of further reducing the number of fundamental forces.

The Gravitational Force (Newton's Law of Universal Gravitation)

Objects fall downward because of gravity, and we discuss how to describe the effects of gravity by using a value of g = 9.8 m/s$^2$ for the downward acceleration it causes. However, nothing has been said about why g is 9.8 m/s$^2$ .

The acceleration due to gravity is like any other acceleration, and Newton's second law indicates that it must be caused by a net force. In addition to his famous three laws of motion, Newton also provided a coherent understanding of the gravitational force. His "law of universal gravitation" is stated as follows:

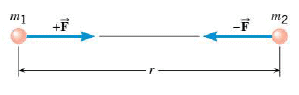Every particle in the universe exerts an attractive force on every other particle. A particle is a piece of matter, small enough in size to be regarded as a mathematical point. For two particles that have masses $m_1$ and $m_2$ and are separated by a distance $r$, the force that each exerts on the other is directed along the line joining the particles and has a magnitude given by

$$F=G \dfrac{m_1 m_2}{r^2}$$

The symbol $G$ denotes the universal gravitational constant, whose value is found experimentally to be $G = 6.674 \times 10^{- 11} \;\mathrm{N · m^2 /kg^2}$

In the figure we see that the gravitational forces point along the line joining the particles and are:

$+ \vec{F}$, the gravitational force exerted on particle 1 by particle 2

$- \vec{F}$, the gravitational force exerted on particle 2 by particle 1

These two forces have equal magnitudes and opposite directions. They act on different bodies, causing them to be mutually attracted. In fact, these forces are an action-reaction pair, as required by Newton's third law. The magnitude of the gravitational force is extremely small for ordinary values of the masses and the distance between them.

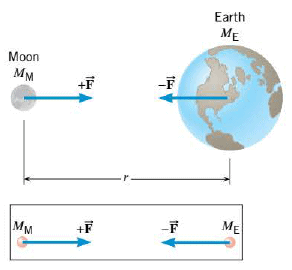Newton's law of gravitation applies only to particles. However, most familiar objects are too large to be considered particles. Nevertheless, the law of universal gravitation can be applied to such objects with the aid of calculus. Newton was able to prove that an object of finite size can be considered to be a particle for purposes of using the gravitation law, provided the mass of the object is distributed with spherical symmetry about its center. Thus, law of universal gravitation can be applied when each object is a sphere whose mass is spread uniformly over its entire volume. The Figure shows this kind of application, assuming that the earth and the moon are such uniform spheres of matter. In this case, $r$ is the distance between the centers of the spheres and not the distance between the outer surfaces. The gravitational forces that the spheres exert on each other are the same as if the entire mass of each were concentrated at its center. Even if the objects are not uniform spheres, law of universal gravitation can be used to a good degree of approximation if the sizes of the objects are small relative to the distance of separation $r$.

 

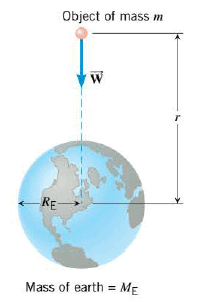The weight of an object on or above the earth is the gravitational force that the earth exerts on the object. The weight always acts downward, toward the center of the earth. On or above another astronomical body, the weight is the gravitational force exerted on the object by that body. SI Unit of Weight: newton (N)

Using $W$ for the magnitude of the weight, $m$ for the mass of the object, and $M_E$ for the mass of the earth, it follows from law of universal gravitation that:

$$W=G \dfrac{M_E m}{r^2}$$

The Figure emphasize that an object has weight whether or not it is resting on the earth's surface, because the gravitational force is acting even when the distance $r$ is not equal to the radius $R_E$ of the earth. However, the gravitational force becomes weaker as $r$ increases, since $r$ is in the denominator of the above Equation.

The space age has forced us to broaden our ideas about weight. For instance, an astronaut weighs only about one-sixth as much on the moon as on the earth. To obtain his weight on the moon from the above Equation, it is only necessary to replace $M_E$ by $M_M$ (the mass of the moon) and let $r = R_M$ (the radius of the moon).

Although massive objects weigh a lot on the earth, mass and weight are not the same quantity.As we see, mass is a quantitative measure of inertia. As such, mass is an intrinsic property of matter and does not change as an object is moved from one location to another. Weight, in contrast, is the gravitational force acting on the object and can vary, depending on how far the object is above the earth's surface or whether it is located near another body such as the moon. The relation between weight Wand mass m can be written in two ways (Newton's law of universal gravitation, and Newton's second law):

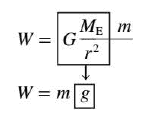
The specific value of g = 9.8 m/s$^2$ applies only when $r$ equals the radius $R_E$ of the earth. For larger values of $r$, as would be the case on top of a mountain, the effective value of g is less than 9.8 m/s$^2$ . The fact that g decreases as the distance $r$ increases means that the weight likewise decreases. The mass of the object, however, does not depend on these effects and does not change.

The Normal Force

In many situations, an object is in contact with a surface, such as a tabletop. Because of the contact, there is a force acting on the object. Here we discusses only one component of this force, the component that acts perpendicular to the surface. Next we will discusses the component that acts parallel to the surface. The perpendicular component is called the normal force.

The normal force $\vec{F_N}$ is one component of the force that a surface exerts on an object with which it is in contact-namely, the component that is perpendicular to the surface.

The Figure shows a block resting on a horizontal table and identifies the two forces that act on the block, the weight $\vec{W}$ and the normal force $\vec{F_N}$. To understand how an inanimate object, such as a tabletop, can exert a normal force, think about what happens when you sit on a mattress. Your weight causes the springs in the mattress to compress. As a result, the compressed springs exert an upward force (the normal force) on you. In a similar manner, the weight of the block causes invisible "atomic springs" in the surface of the table to compress, thus producing a normal force on the block.

Newton's third law plays an important role in connection with the normal force. In the Figure, for instance, the block exerts a force on the table by pressing down on it. Consistent with the third law, the table exerts an oppositely directed force of equal magnitude on the block. This reaction force is the normal force. The magnitude of the normal force indicates how hard the two objects press against each other.

If an object is resting on a horizontal surface and there are no vertically acting forces except the object's weight and the normal force, the magnitudes of these two forces are equal; that is, $F_N = W$. This is the situation in the Figure. The weight must be balanced by the normal force for the object to remain at rest on the table. If the magnitudes of these forces were not equal, there would be a net force acting on the block, and the block would accelerate either upward or downward, in accord with Newton's second law.

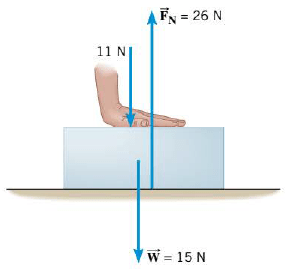If other forces in addition to $\vec{W}$ and $\vec{F_N}$ act in the vertical direction, the magnitudes of the normal force and the weight are no longer equal. In Figure, for instance, a box whose weight is 15 N is being pushed downward against a table. The pushing force has a magnitude of 11 N. Thus, the total downward force exerted on the box is 26 N, and this must be balanced by the upward-acting normal force if the box is to remain at rest. In this situation, then, the normal force is 26 N, which is considerably larger than the weight of the box.

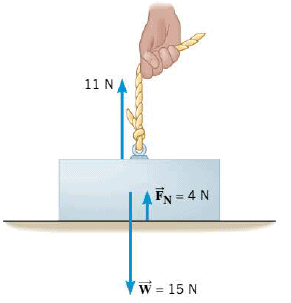This Figure illustrates a different situation. Here, the box is being pulled upward by a rope that applies a force of 11 N. The net force acting on the box due to its weight and the rope is only 4 N, downward. To balance this force, the normal force needs to be only 4 N. It is not hard to imagine what would happen if the force applied by the rope were increased to 15 N-exactly equal to the weight of the box. In this situation, the normal force would become zero. In fact, the table could be removed, since the block would be supported entirely by the rope.

The situations in the above are consistent with the idea that the magnitude of the normal force indicates how hard two objects press against each other. Clearly, the box and the table press against each other harder in the first figure than in the second figure.

In summary, the normal force does not necessarily have the same magnitude as the weight of the object. The value of the normal force depends on what other forces are present. It also depends on whether the objects in contact are accelerating. In one situation that involves accelerating objects, the magnitude of the normal force can be regarded as a kind of "apparent weight".

 

Usually, the weight of an object can be determined with the aid of a scale. However, even though a scale is working properly, there are situations in which it does not give the correct weight. In such situations, the reading on the scale gives only the "apparent" weight~ rather than the gravitational force or "true" weight. The apparent weight is the force that the object exerts on the scale with which it is in contact.

To see the discrepancies that can arise between true weight and apparent weight, consider the scale in the elevator in the figure:

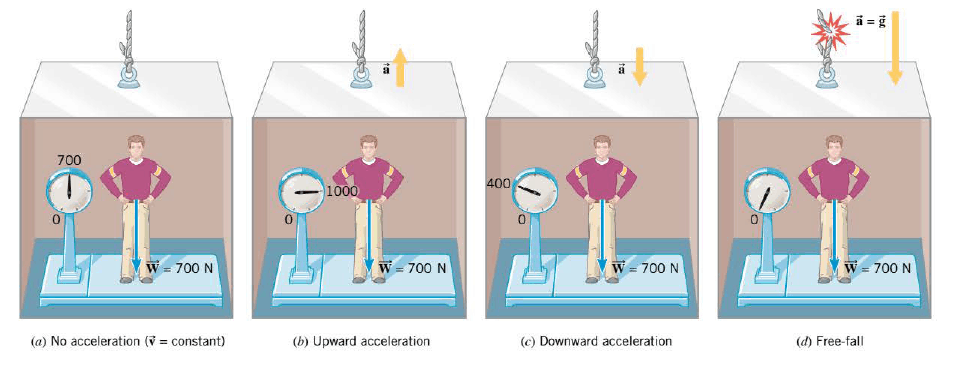
A person whose true weight is 700 N steps on the scale. If the elevator is at rest or moving with a constant velocity ( either upward or downward), the scale registers the true weight, as the above Figure illustrates.

If the elevator is accelerating, the apparent weight and the true weight are not equal. When the elevator accelerates upward, the apparent weight is greater than the true weight, as the Figure shows. Conversely, if the elevator accelerates downward, the apparent weight is less than the true weight. In fact, if the elevator falls freely, so its acceleration is equal to the acceleration due to gravity, the apparent weight becomes zero. In a situation such as this, where the apparent weight is zero, the person is said to be "weightless." The apparent weight, then, does not equal the true weight if the scale and the person on it are accelerating.

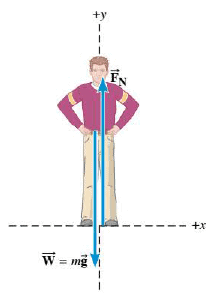The discrepancies between true weight and apparent weight can be understood with the aid of Newton's second law. This Figure shows a free-body diagram of the person in the elevator. The two forces that act on him are the true weight $\vec{W}=m \vec{g}$ and the normal force $\vec{F_N}$ exerted by the platform of the scale. Applying Newton's second law in the vertical direction gives:

$$\sum F_y = +F_N - mg = ma$$

where $a$ is the acceleration of the elevator and person. In this result, the symbol $g$ stands for the magnitude of the acceleration due to gravity and can never be a negative quantity. However, the acceleration $a$ may be either positive or negative, depending on whether the elevator is accelerating upward (+) or downward (-). Solving for the normal force $F_N$ shows that:

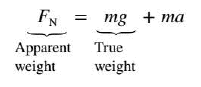
This Equation contains all the features shown in the elevator Figure. If the elevator is not accelerating, a = 0 m/s$^2$ , and the apparent weight equals the true weight. If the elevator accelerates upward, a is positive, and the equation shows that the apparent weight is greater than the true weight. If the elevator accelerates downward, a is negative, and the apparent weight is less than the true weight. If the elevator falls freely, a= - g, and the apparent weight is zero. The apparent weight is zero because when both the person and the scale fall freely, they cannot push against one another.

Static and Kinetic Frictional Forces

When an object is in contact with a surface, there is a force acting on the object. The previous section discusses the component of this force that is perpendicular to the surface, which is called the normal force. When the object moves or attempts to move along the surface, there is also a component of the force that is parallel to the surface. This parallel force component is called the frictional force, or simply friction.

In many situations considerable engineering effort is expended trying to reduce friction. For example, oil is used to reduce the friction that causes wear and tear in the pistons and cylinder walls of an automobile engine. Sometimes, however, friction is absolutely necessary. Without friction, car tires could not provide the traction needed to move the car. In fact, the raised tread on a tire is designed to maintain friction. On a wet road, the spaces in the tread pattern provide channels for the water to collect and be diverted away. Thus, these channels largely prevent the water from coming between the tire surface and the road surface, where it would reduce friction and allow the tire to skid.

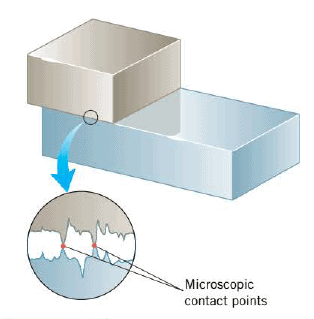Surfaces that appear to be highly polished can actually look quite rough when examined under a microscope. Such an examination reveals that two surfaces in contact touch only at relatively few spots, as the Figure illustrates. The microscopic area of contact for these spots is substantially less than the apparent macroscopic area of contact between the surfaces- perhaps thousands of times less. At these contact points the molecules of the different bodies are close enough together to exert strong attractive intermolecular forces on one another, leading to what are known as "cold welds." Frictional forces are associated with these welded spots, but the exact details of how frictional forces arise are not well understood. However, some empirical relations have been developed that make it possible to account for the effects of friction.

The following Figure helps to explain the main features of the type of friction known as static friction.

The block in this drawing is initially at rest on a table, and as long as there is no attempt to move the block, there is no static frictional force. Then, a horizontal force $\vec{F}$ is applied to the block by means of a rope. If $\vec{F}$ is small, as in part a, experience tells us that the block still does not move. Why? It does not move because the static frictional force $\vec{f_s}$ exactly cancels the effect of the applied force. The direction of $\vec{f_s}$ is opposite to that of $\vec{F}$, and the magnitude of $\vec{f_s}$ equals the magnitude of the applied force, $f_s = F$. Increasing the applied force in the Figure by a small amount still does not cause the block to move. There is no movement because the static frictional force also increases by an amount that cancels out the increase in the applied force (see part b of the drawing). If the applied force continues to increase, however, there comes a point when the block finally "breaks away" and begins to slide. The force just before breakaway represents the maximum static frictional force $\vec{f_s}^{MAX}$ that the table can exert on the block (see part c of the drawing). Any applied force that is greater than $\vec{f_s}^{MAX}$ cannot be balanced by static friction, and the resulting net force accelerates the block to the right.

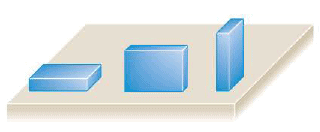Experimental evidence shows that, to a good degree of approximation, the maximum static frictional force between a pair of dry, unlubricated surfaces has two main characteristics. It is independent of the apparent macroscopic area of contact between the objects, provided that the surfaces are hard or nondeformable. For instance, in the Figure the maximum static frictional force that the surface of the table can exert on a block is the same, whether the block is resting on its largest or its smallest side. The other main characteristic of $\vec{f_s}^{MAX}$ is that its magnitude is proportional to the magnitude of the normal force $\vec{F_N}$. Then, the magnitude of the normal force indicates how hard two surfaces are being pressed together. The harder they are pressed, the larger is $f_s^{MAX}$, presumably because the number of "cold-welded," microscopic contact points is increased. The following Equation expresses the proportionality between $f_s^{MAX}$ and $F_N$ with the aid of a proportionality constant $\mu_s$, which is called the coefficient of static friction.

The magnitude of the static frictional force $f_s$ can have any value from zero up to a maximum value of $f_s^{MAX}$, depending on the applied force. In other words, $f_s \leq f_s^{MAX}$, where the symbol $\leq $ is read as "less than or equal to". The equality holds only when $f_s$ attains its maximum value, which is

$$f_s^{MAX} = \mu_s F_N$$

It should be emphasized that this Equation relates only the magnitudes of $\vec{f_s^{MAX}}$ and $\vec{F_N}$, not the vectors themselves. This equation does not imply that the directions of the vectors are the same. In fact, $\vec{f_s^{MAX}}$ is parallel to the surface, while $\vec{F_N}$ is perpendicular to it.

 

Experimental evidence indicates that the kinetic frictional force $\vec{f_k}$ has three main characteristics, to a good degree of approximation. It is independent of the apparent area of contact between the surfaces. It is independent of the speed of the sliding motion, if the speed is small. And last, the magnitude of the kinetic frictional force is proportional to the magnitude of the normal force. The following Equation expresses this proportionality with the aid of a proportionality constant $\mu_k$, which is called the coefficient of kinetic friction.

The magnitude $f_k$ of the kinetic frictional force is given by

$$f_k = \mu_k F_N$$

And values for $\mu_k$ are typically less than those for $\mu_s$, reflecting the fact that kinetic friction is generally less than static friction.

Static friction opposes the impending relative motion between two objects, while kinetic friction opposes the relative sliding motion that actually does occur. In either case, relative motion is opposed. However, this opposition to relative motion does not mean that friction prevents or works against the motion of all objects. For instance, consider what happens when you walk. Your foot exerts a force on the earth, and the earth exerts a reaction force on your foot. This reaction force is a static frictional force, and it opposes the impending backward motion of your foot, propelling you forward in the process. Kinetic friction can also cause an object to move, all the while opposing relative motion, as it does in Example 10. In this example the kinetic frictional force acts on the sled and opposes the relative motion of the sled and the earth. Newton's third law indicates, however, that since the earth exerts the kinetic frictional force on the sled, the sled must exert a reaction force on the earth. In response, the earth accelerates, but because of the earth's huge mass, the motion is too slight to be noticed.

The Tension Force

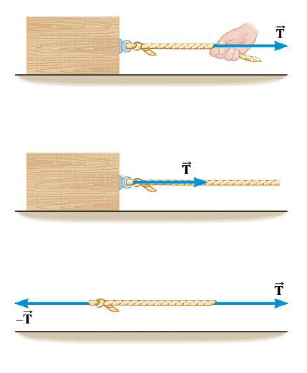Forces are often applied by means of cables or ropes that are used to pull an object. For instance, the Figure shows a force $\vec{T}$ being applied to the right end of a rope attached to a box. Each particle in the rope in turn applies a force to its neighbor. As a result, the force is applied to the box, as the second drawing shows. In situations such as that in the Figure, we say that the force $\vec{T}$ is applied to the box because of the tension in the rope, meaning that the tension and the force applied to the box have the same magnitude. However, the word "tension" is commonly used to mean the tendency of the rope to be pulled apart. To see the relationship between these two uses of the word "tension," consider the left end of the rope, which applies the force $\vec{T}$ to the box. In accordance with Newton's third law, the box applies a reaction force to the rope. The reaction force has the same magnitude as $\vec{T}$ but is oppositely directed. In other words, a force $-\vec{T}$ acts on the left end of the rope. Thus, forces of equal magnitude act on opposite ends of the rope, as the third drawing shows, and tend to pull it apart.

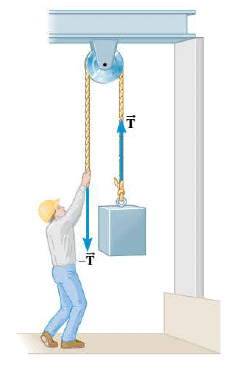In the previous discussion, we have used the concept of a "massless" rope (m = 0 kg) without saying so. In reality, a massless rope does not exist, but it is useful as an idealization when applying Newton's second law. According to the second law, a net force is required to accelerate an object that has mass. In contrast, no net force is needed to accelerate a massless rope, since : $\sum \vec{F}= m \vec{a}$ and m = 0 kg. Thus, when a force $\vec{T}$ is applied to one end of a massless rope, none of the force is needed to accelerate the rope. As a result, the force $\vec{T}$ is also applied undiminished to the object attached at the other end, as we assumed in the previous discussion. If the rope had mass, however, some of the force $\vec{T}$ would have to be used to accelerate the rope. The force applied to the box would then be less than $\vec{T}$ , and the tension would be different at different locations along the rope. Here we will assume that a rope connecting one object to another is massless, unless stated otherwise. The ability of a massless rope to transmit tension undiminished from one end to the other is not affected when the rope passes around objects such as the pulley in the Figure (provided the pulley itself is massless and frictionless).