We saw in that the concept of energy was extremely valuable in dealing with the subject of mechanics. For one thing, energy is a conserved quantity and is thus an important tool for understanding nature. Furthermore, we saw that many Problems could be solved using the energy concept even though a detailed knowledge of the forces involved was not possible, or when a calculation involving Newton’s laws would have been too difficult.

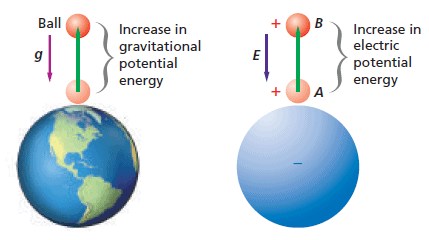
The energy point of view can be used in electricity, and it is especially useful. It not only extends the law of conservation of energy, but it gives us another way to view electrical phenomena. The energy concept is also a tool in solving Problems more easily in many cases than by using forces and electric fields.

To apply conservation of energy, we need to define electric potential energy as we did for other types of potential energy. We knowe that potential energy can be defined only for a conservative force. The electrostatic force between any two charges $\left( F= k \dfrac{\left | q_1 \right | \left | q_2 \right |}{r^2} \right)$ is conservative because the dependence on position is just like the gravitational force $\left( F= G \dfrac{m_1 m_2}{r^2} \right)$, which is conservative. Hence we can define potential energy for the electrostatic force.

We also saw that the work done by a conservative force in moving an object between any two positions is independent of the path taken. And we knows that the change in potential energy between any two points, A and B, equals the negative of the work done by the conservative force on an object as it moves from point A to point B: $\Delta PE = -W$

Consider the electric field between two equally but oppositely charged parallel plates; we assume their separation is small compared to their width and height, so the field $\vec{E}$ will be uniform over most of the region. Now consider a tiny positive point charge $q_0$ placed at the point “A” very near the positive plate. This charge $q_0$ is so small that it has no effect on $\vec{E}$.

If this charge $q_0$ at point A is released, the electric force will do work on the charge and accelerate it toward the negative plate. The work $W$ done by the electric field $E$ to move the charge a distance $d$ To the point B is $W_{AB}= Fd= q_0Ed$, and the change in electric potential energy equals the negative of the work done by the electric force:

$$ -W_{AB} = EPE_B - EPE_A $$ $$W_{AB} = EPE_A - EPE_B$$

In the case illustrated, the potential energy decreases ( is negative); and as the charged particle accelerates from point A to point B, the particle’s kinetic energy KE increases—by an equal amount. In accord with the conservation of energy, electric potential energy is transformed into kinetic energy, and the total energy is conserved.

Note that the positive charge $q_0$ has its greatest potential energy at point A, near the positive plate(At point A, the positive charge $q_0$ has its greatest ability to do work -on some other object or system). The reverse is true for a negative charge: its potential energy is greatest near the negative plate.

Electric Potential

Since the work that that the electric force does as the charge moves from A to B ($W_{AB}= q_0Ed$) in depends on the charge $q_0$. It is useful, therefore, to express this work on a per-unit-charge basis, by dividing both sides of the above Equation by the charge:

$$\dfrac{-W_{AB}}{q_0} = \dfrac{EPE_B}{q_0} - \dfrac{EPE_A}{q_0}$$

The quantity ($EPE/q_0$) is the electric potential energy per unit charge and it is called the electric potential or, simply, the potential and is referred to with the symbol $V$:

$$\dfrac{-W_{AB}}{q_0} = V_B - V_A$$

The electric potential $V$ at a given point is the electric potential energy $EPE$ (relative to some zero potential energy) of a small test charge $q_0$ situated at that point divided by the charge itself:

$$V= \dfrac{EPE}{q_0}$$

SI Unit of Electric Potential: joule/coulomb = volt (V)

In spite of the similarity in names, the electric potential energy $EPE$ and the electric potential $V$ are not the same. The electric potential energy, as its name implies, is an energy and, therefore, is measured in joules. In contrast, the electric potential is an energy per unit charge and is measured in joules per coulomb, or volts.

We can see from our definition that the positive plate is at a higher potential than the negative plate. Thus a positively charged object moves naturally from a high potential to a low potential. A negative charge does the reverse.

Note that, the positive charge accelerates as it moves from A to B because of the electric repulsion from the positive plate and the attraction to the nigative plate. Since point A has a higher electric potential than point B, we conclude that a positive charge accelerates from a region of higher electric potential toward a region of lower electric potential.

On the other hand, a negative charge placed between the plates behaves in the opposite fashion, since the electric force acting on the negative charge is directed opposite to the electric force acting on the positive charge. So, a negative charge accelerates from a region of lower potential toward a region of higher potential.

Note that electric potential, like electric field, does not depend on our test charge $q_0$. $V$ depends on the other charges that create the field, not on the test charge $q_0$; $q_0$ acquires potential energy by being in the potential $V$ due to the other charges.

As we saw before, only differences in potential energy ($\Delta PE$) are physically meaningful. Hence only the difference in potential($\Delta V$), or the potential difference, between two points A and B is measurable.

When the electric force does positive work on a charge, the kinetic energy increases and the potential energy decreases. The difference in potential energy, $EPE_B - EBE_A$, is equal to the negative of the work, $W_{AB}$, done by the electric field to move the charge from A to B; so:

$$-W_{AB}= \Delta EPE = EPE_B - EBE_A$$ $$\dfrac{-W_{AB}}{q_0} = \dfrac{\Delta EPE}{q_0} = \dfrac{EPE_B}{q_0} - \dfrac{EPE_A}{q_0} = V_B - V_A$$

Often, the "delta" notation is used to express the difference (final value minus initial value). In terms of this notation, Equation takes the following more compact form:

$$\dfrac{-W_{AB}}{q_0} = \Delta V$$

The potential difference between two points is measured in volts and, therefore, is often referred to as a "voltage." Everyone has heard of "voltage" because it is frequently used in connection with everyday devices. For example, your TV requires a "voltage" of 120 V (which is applied between the two prongs of the plug on the power cord when it is inserted into an electrical wall outlet), and your cell phone and laptop computer use batteries that provide, for example, "voltages" of 1.5 V or 9 V (which exist between the two battery terminals).

Neither the potential $V$ nor the potential energy $EPE$ can be determined in an absolute sense, because only the differences $\Delta V$ and $\Delta EPE$ are measurable in terms of the work $W_{AB}$· The gravitational potential energy has this same characteristic, since only the value at one height relative to the value at some reference height has any significance.

If we wish to speak of the potential $V_A$ at some point A, we must be aware that $V_A$ depends on where the potential is chosen to be zero. The zero for electric potential in a given situation can be chosen arbitrarily, just as for potential energy, because only differences in potential energy can be measured. Often the ground, or a conductor connected directly to the ground (the Earth), is taken as zero potential, and other potentials are given with respect to ground. (Thus, a point where the voltage is 50 V is one where the difference of potential between it and ground is 50 V.) In other cases, as we shall see, we may choose the potential to be zero at an infinite distance.

As a familiar application of electric potential energy and electric potential, take a 12-V automobile battery with a headlight connected between its terminals. The positive terminal, point A, has a potential that is 12 V higher than the potential at the negative terminal, point B; in other words, $V_A - V_B = 12$ V. Positive charges would be repelled from the positive terminal and would travel through the wires and headlight toward the negative terminal (conventional electric current). As the charges pass through the headlight, virtually all their potential energy is converted into heat, which causes the filament to glow "white hot" and emit light. When the charges reach the negative terminal, they no longer have any potential energy. The battery then gives the charges an additional "shot" of potential energy by moving them to the higher-potential positive terminal, and the cycle is repeated. In raising the potential energy of the charges, the battery does work on them and draws from its reserve of chemical energy to do so.

The change in potential energy of a charge $q_0$ when it moves from point A to point B is:

$$\Delta EPE = EPE_B - EPE_A = q_0 \Delta V$$

For example, if the potential difference between the two plates is 6 V, then a +1C charge moved from point B to point A will gain (1 x 6 = 6 J) of electric potential energy. (And it will lose 6 J of electric potential energy if it moves from A to B). Thus, electric potential difference is a measure of how much energy an electric charge can acquire in a given situation. And, since energy is the ability to do work, the electric potential difference is also a measure of how much work a given charge can do. The exact amount of energy or work depends both on the potential difference and on the charge.

The Electric Potential Difference Created by Point Charges

A positive point charge $+q$ creates an electric potential. Take two locations A and B, at distances $r_A$ and $r_B$ from the charge. At any position between A and B an electrostatic force of repulsion $\vec{F}$ acts on a positive test charge $+q_0$. The magnitude of the force is given by Coulomb's law as $F = k q_0 q/r_2$, where we assume for convenience that $q_0$ and $q$ are positive, so that $\left | q_0 \right | = q_0$ and $\left | q \right | = q$. When the test charge moves from A to B, work is done by this force. Since $r$ varies between $r_A$ and $r_B$, the force $F$ also varies, and the work is not the product of the force and the distance between the points. (Recall that work is force times distance only if the force is constant.) However, the work $W_{AB}$ can be found with the methods of integral calculus. The result is:

$$W_{AB} = \dfrac{kqq_0}{r_A} -\dfrac{k qq_0}{r_B}$$

This result is valid whether $q$ is positive or negative, and whether $q_0$ is positive or negative. The potential difference, $V_B - V_A$ between A and B can now be determined by substituting this expression for $W_{AB}$ into the Equation $\left( \dfrac{-W_{AB}}{q_0} = \Delta V \right)$:

$$ V_B -V_A= \dfrac{-W_{AB}}{q_0} = \dfrac{kq}{r_B} - \dfrac{kq}{r_A}$$

As point B is located farther and farther from the charge $q$, $r_B$ becomes larger and larger. In the limit that $r_B$ is infinitely large, the term $kq/r_B$ becomes zero, and it is customary to set $V_B$ equal to zero also. In this limit, this Equation becomes $V_A= kq/r_A$, and it is standard convention to omit the subscripts and write the Potential in the following form:

$$V = \dfrac{kq}{r}$$

The symbol $V$ in this equation does not refer to the potential in any absolute sense. Rather, $V = kq/ r$ stands for the amount by which the potential at a distance $r$ from a point charge differs from the potential at an infinite distance away. In other words, $V$ refers to a potential difference with the arbitrary assumption that the potential at infinity is zero.

With the aid of this Equation, we can describe the effect that a point charge $q$ has on the surrounding space. When $q$ is positive, the value of $V = kq/r$ is also positive, indicating that the positive charge has everywhere raised the potential above the zero reference value. Conversely, when $q$ is negative, the potential $V$ is also negative, indicating that the negative charge has everywhere decreased the potential below the zero reference value.

A single point charge raises or lowers the potential at a given location, depending on whether the charge is positive or negative.

When two or more charges are present, the potential due to all the charges is obtained by adding together the individual potentials.

Potential Due to Electric Dipole; Dipole Moment

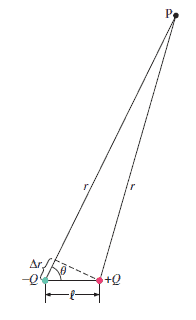Two equal point charges $q$, of opposite sign, separated by a distance are called an electric dipole. Because electric dipoles occur often in physics, as well as in other disciplines such as molecular biology, it is useful to examine them more closely.

The electric potential due to a dipole at an arbitrary point P is the sum of the potentials due to each of the two charges, and if the point P distance from the dipole is much larger than the separation of the two charges, $ r \gg l $, we obtine:

$$V \approx \dfrac{Kql \cos \theta}{r^2} \;\;\;\;\;\;\;\;\; [\text{dipole} , r \gg l]$$

We see that the potential decreases as the square of the distance from the dipole, whereas for a single point charge the potential decreases with the first power of the distance (as the equation $V=kq/r$ states). It is not surprising that the potential should fall off faster for a dipole: when you are far from a dipole, the two equal but opposite charges appear so close together as to tend to neutralize each other. The product $ql$ in the above equation is referred to as the dipole moment, $p$, of the dipole. the above Equation in terms of the dipole moment is:

$$V \approx \dfrac{Kp \cos \theta}{r^2} \;\;\;\;\;\;\;\;\; [\text{dipole} , r \gg l]$$

Equipotential Surfaces and Their Relation to the Electric Field

An equipotential surface is a surface on which the electric potential is the same everywhere. The easiest equipotential surfaces to visualize are those that surround an isolated point charge. According to above, the potential at a distance $r$ from a point charge q is $V = kq/r$. Thus, wherever $r$ is the same, the potential is the same, and the equipotential surfaces are spherical surfaces centered on the charge. There are an infinite number of such surfaces, one for every value of $r$. The larger the distance $r$, the smaller is the potential of the equipotential surface.

The net electric force does no work as a charge moves on an equipotential surface.

The Electron Volt, a Unit of Energy

As used in connection with batteries, the volt is a familiar unit for measuring electric potential difference. The word "volt" also appears in another context, as part of a unit that is used to measure energy, particularly the energy of an atomic particle, such as an electron or a proton. This energy unit is called the electron volt (eV).

A capacitor is a device that can store electric charge, and normally consists of two conducting objects (usually plates or sheets) placed near each other but not touching. Capacitors are widely used in electronic circuits and sometimes are called condensers. Capacitors store charge for later use, such as in a camera flash, and as energy backup in devices like computers if the power fails. Capacitors also block surges of charge and energy to protect circuits. Very tiny capacitors serve as memory for the “ones” and “zeros” of the binary code in the random access memory (RAM) of computers and other electronic devices. Capacitors serve many other applications as well, some of which we will discuss.

Capacitance

A capacitor stores electric charge. Each capacitor plate carries a charge of the same magnitude, one positive and the other negative. Because of the charges, the electric potential of the positive plate exceeds that of the negative plate by an amount $V$. Experiment shows that when the magnitude $q$ of the charge on each plate is doubled, the magnitude $V$ of the electric potential difference is also doubled, so $q$ is proportional to $V$: $q \propto V$. We can expresses this proportionality with the aid of a proportionality constant $C$, which is the capacitance of the capacitor, by the equation:

$$ q=CV$$

This Equation shows that the SI unit of capacitance is the coulomb per volt (C/V). This unit is called the farad (F), named after the English scientist Michael Faraday (1791-1867). One farad is an enormous capacitance. Usually smaller amounts, such as a microfarad ($1 \mu F = 10^{-6 F}$) or a picofarad ( $l pF = 10^{- 12} F$), are used in electric circuits. The capacitance reflects the ability of the capacitor to store charge, in the sense that a larger capacitance $C$ allows more charge $q$ to be put onto the plates for a given value of the potential difference $V$.

Dielectrics

If a dielectric is inserted between the plates of a capacitor, the capacitance can increase markedly because of the way in which the dielectric alters the electric field between the plates.

The Capacitance of a Parallel Plate Capacitor

The capacitance of a capacitor is affected by the geometry of the plates and the dielectric constant of the material between them

Storage of Electric Energy

When a capacitor stores charge, it also stores energy. In charging up a capacitor, for example, a battery does work in transferring an increment of charge from one plate of the capacitor to the other plate. The work done is equal to the product of the charge increment and the potential difference between the plates. However, as each increment of charge is moved, the potential difference increases slightly, and a larger amount of work is needed to move the next increment. The total work $W$ done in completely charging the capacitor is the product of the total charge $q$ transferred and the average potential difference $V$; $W = qV$. Since the average potential difference is one-half the final potential $V$, or $V = \frac{1}{2} V$, the total work done by the battery is $W = \frac{1}{2} qV$. This work does not disappear but is stored as electric potential energy in the capacitor, so that Energy $= \frac{1}{2} qV$. Above Equation indicates that $q = CV$ or, equivalently, that $V = q/C$. We can see, then, that our expression for the energy can be cast into two additional equivalent forms by substituting for $q$ or for $V$.