Fluids Statics and Dynamics
Fluids are materials that can flow, and they include both gases and liquids. Air is the most common gas, and flows from place to place as wind. Water is the most familiar liquid, and flowing water has many uses, from generating hydroelectric power to white-water rafting, we will learn about the principles that explain how fluids responds to changes in temperature and pressure, how hydraulic systems can multiply forces, and how huge metallic ships can float on water.
We also will investigate the properties of solids, discovering how they expand and contract, why some solids are elastic, and why some solids seem to straddle the line between solid and liquid.
Digital lesson: What Are Solids, Liquids, And Gases?
|
Digital lesson: How Can Matter Change?
|
Digital Lab: How Can We Change Matter?
|
|---|---|---|
Digital lesson: What Are The States of matter?
|
Digital lesson: What Are Some Changes To Matter?
|
Digital Lab: What Changes Can We Observe?
|
Digital lesson: What Are The States Of Water?
|
Digital lesson: What Are Some Physical Changes?
|
Digital lesson: How Does Matter Changes?
|
Digital lesson: States Of Matter
|
Digital Lab: Change Of Pace
|
Properties of Matter
Mass Density
The mass density is the mass per unit volume and is denoted by the Greek letter rho ($\rho$).
A convenient way to compare densities is to use the concept of specific gravity. The specific gravity of a substance is its density divided by the density of a standard reference material, usually chosen to be water at 4°C.
Pressure
People who have fixed a flat tire know something about pressure. The final step in the job is to reinflate the tire to the proper pressure. The underinflated tire is soft because it contains an insufficient number of air molecules to push outward against the rubber and give the tire that solid feel.
When air is added from a pump, the number of molecules and the collective force they exert are increased. The air molecules within a tire are free to wander throughout its entire volume, and in the course of their wandering they collide with one another and the inner walls of the tire. The collisions with the walls allow the air to exert a force against every part of the wall surface. The pressure P exerted by a fluid is defined as the magnitude F of the force acting perpendicular to a surface divided by the area A over which the force acts.
Because of its pressure, the air in a tire applies a force to any surface with which the air is in contact. Suppose, for instance, that a small cube is inserted inside the tire, the air pressure causes a force to act perpendicularly on each face of the cube. In a similar fashion, a liquid such as water also exerts pressure. A swimmer, for example, feels the water pushing perpendicularly inward everywhere on her body. In general, a static fluid cannot produce a force parallel to a surface, for if it did, the surface would apply a reaction force to the fluid, consistent with Newton's action-reaction law. In response, the fluid would flow and would not then be static.
While fluid pressure can generate a force, which is a vector quantity, pressure itself is not a vector. In the definition of pressure, P = F/A, the symbol F refers only to the magnitude of the force, so that pressure has no directional characteristic. The force generated by the pressure of a static fluid is always perpendicular to the surface that the fluid contacts.
Relate Pressure and Depth in a Static Fluid
The deeper an underwater swimmer goes, the more strongly the water pushes on his body and the greater is the pressure that he experiences. To determine the relation between pressure and depth, we turn to Newton's second law (F = ma). In using the second law, we will focus on two external forces that act on the fluid. One is the gravitational force-that is, the weight of the fluid. The other is the collisional force that is responsible for fluid pressure. Since the fluid is at rest, its acceleration is zero (a = 0 m/s2), and it is in equilibrium.
By applying the second law in the form F = 0, we will derive a relation between pressure and depth. This relation is especially important because it leads to Pascal's principle and Archimedes' principle, both of which are essential in describing the properties of static fluids.
Gauge, Atmospheric, and Absolute Pressures
A person need not be under water to experience the effects of pressure. Walking about on land, we are at the bottom of the earth's atmosphere, which is a fluid and pushes inward on our bodies just like the water in a swimming pool. There is enough air above the surface of the earth to create the following pressure at sea level: $1.013 \times 10^5$ Pa= 1 atmosphere
This pressure corresponds to 14.70 $lb/in.^2$ and is referred to as one atmosphere (atm), a significant amount of pressure.
One of the simplest pressure gauges is the mercury barometer used for measuring atmospheric pressure. This device is a tube sealed at one end, filled completely with mercury, and then inverted, so that the open end is under the surface of a pool of mercury. Except for a negligible amount of mercury vapor, the space above the mercury in the tube is empty, and the pressure P1 is nearly zero there.
The gauge pressure is the amount by which the container pressure differs from atmospheric pressure. The actual value of the pressure at the mercury surface is called the absolute pressure.
Interactive Demonstration: Pressure
|
Digital Figure: container of fluid
|
Digital lesson: What Is Matter?
|
|---|---|---|
Digital Lab: How Can We Compare Volumes?
|
Digital Lab: What Physical Properties Can We Observe?
|
Digital Lesson: What Are Physical Properties Of Matter?
|
Digital Lab: How Are Physical Properties Observed?
|
Digital lesson: Introduction To Matter
|
Digital lesson: Properties Of Matter
|
Digital Lab: Determining Density
|
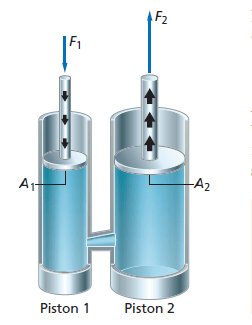
Pascal's Principle
As we have seen, the pressure in a fluid increases with depth, due to the weight of the fluid above the point of interest. A completely enclosed fluid may be subjected to an additional pressure by the application of an external force. This behavior is described by Pascal's principle:
Any change in the pressure applied to a completely enclosed fluid is transmitted undiminished to all parts of the fluid and the enclosing walls.
Animated Physics: Pascal's Principle
|
|---|
Archimedes' Principle
Anyone who has tried to push a beach ball under the water has felt how the water pushes back with a strong upward force. This upward force is called the buoyant force, and all fluids apply such a force to objects that are immersed in them. The buoyant force exists because fluid pressure is larger at greater depths. The shape of the object is not important. No matter what its shape, the buoyant force pushes it upward in accord with Archimedes' principle. It was an impressive accomplishment that the Greek scientist Archimedes (ca. 287-212 BC) discovered the essence of this principle so long ago:
Any fluid applies a buoyant force to an object that is partially or completely immersed in it; the magnitude of the buoyant force equals the weight of the fluid that the object displaces.
Animated Physics: Density and Buoyant Force
|
Interactive Demonstration: Buoyant Force
|
Digital Figure: Fluid applies a force
|
|---|---|---|
Digital lesson: Fluids And Pressure?
|
The Equation of Continuity
Fluids can move or flow in many ways. Water may flow smoothly and slowly in a quiet stream or violently over a waterfall. The air may form a gentle breeze or a raging tornado. To deal with such diversity, it helps to identify some of the basic types of fluid flow.
Fluids in Motion
Fluid flow can be steady or unsteady. In steady flow the velocity of the fluid particles at any point is constant as time passes. For instance, a fluid particle flows with a velocity of v1 = + 2 m/s past point 1. In steady flow every particle passing through this point has this same velocity. At another location the velocity may be different, as in a river, which usually flows fastest near its center and slowest near its banks. Thus, at point 2, the fluid velocity is v2 = +0.5 m/s, and if the flow is steady, all particles passing through this point have a velocity of +0.5 m/s. Unsteady flow exists whenever the velocity at a point in the fluid changes as time passes. Turbulent flow is an extreme kind of unsteady flow and occurs when there are sharp obstacles or bends in the path of a fast-moving fluid. In turbulent flow, the velocity at a point changes erratically from moment to moment, both in magnitude and in direction.
Fluid flow can be compressible or incompressible. Most liquids are nearly incompressible; that is, the density of a liquid remains almost constant as the pressure changes. To a good approximation, then, liquids flow in an incompressible manner. In contrast, gases are highly compressible. However, there are situations in which the density of a flowing gas remains constant enough that the flow can be considered incompressible.
Fluid flow can be viscous or nonviscous. A viscous fluid, such as honey, does not flow readily and is said to have a large viscosity. In contrast, water is less viscous and flows more readily; water has a smaller viscosity than honey. The flow of a viscous fluid is an energydissipating process. The viscosity hinders neighboring layers of fluid from sliding freely past one another. A fluid with zero viscosity flows in an unhindered manner with no dissipation of energy. Although no real fluid has zero viscosity at normal temperatures, some fluids have negligibly small viscosities. An incompressible, nonviscous fluid is called an ideal fluid.
When the flow is steady, streamlines are often used to represent the trajectories of the fluid particles. A streamline is a line drawn in the fluid such that a tangent to the streamline at any point is parallel to the fluid velocity at that point. The fluid velocity can vary (in both magnitude and direction) from point to point along a streamline, but at any given point, the velocity is constant in time, as required by the condition of steady flow. In fact, steady flow is often called streamline flow.
The Equation of Continuity
Have you ever used your thumb to control the water flowing from the end of a hose, If so, you have seen that the water velocity increases when your thumb reduces the crosssectional area of the hose opening. This kind of fluid behavior is described by the equation of continuity. This equation expresses the following simple idea: If a fluid enters one end of a pipe at a certain rate (e.g., 5 kilograms per second), then fluid must also leave at the same rate, assuming that there are no places between the entry and exit points to add or remove fluid. The mass of fluid per second (e.g., 5 kg/s) that flows through a tube is called the mass flow rate.
The equation of continuity is an expression of the fact that mass is conserved (i.e., neither created nor destroyed) as the fluid flows:
The mass flow rate ($\rho Av$) has the same value at every position along a tube that has a single entry and a single exit point for fluid flow. For two positions along such a tube
Viscous Flow
In an ideal fluid there is no viscosity to hinder the fluid layers as they slide past one another. Within a pipe of uniform cross section, every layer of an ideal fluid moves with the same velocity, even the layer next to the wall. When viscosity is present, the fluid layers have different velocities. The fluid at the center of the pipe has the greatest velocity. In contrast, the fluid layer next to the wall surface does not move at all, because it is held tightly by intermolecular forces. So strong are these forces that if a solid surface moves, the adjacent fluid layer moves along with it and remains at rest relative to the moving surface.
The magnitude of the tangential force F required to move a ftuid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance y from an immobile surface, is given by:
$$ F= \dfrac{\eta A v}{y}$$
where $\eta$ is the coefficient of viscosity.
The mathematical relation for Q in terms of these parameters was discovered by Poiseuille and is known as Poiseuille's law.
Digital simulations: Continuity Equation
|
|---|
Bernoulli's Equation
For steady flow, the speed, pressure, and elevation of an incompressible and nonviscous fluid are related by an equation discovered by Daniel Bernoulli ( 1700-1782). To derive Bernoulli's equation, we will use the work-energy theorem. This theorem, states that the net work $W_{nc}$ done on an object by external nonconservative forces is equal to the change in the total mechanical energy of the object. As mentioned earlier, the pressure within a fluid is caused by collisional forces, which are nonconservative. Therefore, when a fluid is accelerated because of a difference in pressures, work is being done by nonconservative forces ($W_{nc} \neq 0 J$ ), and this work changes the total mechanical energy of the fluid from an initial value of $E_0$ to a final value of $E_f$. The total mechanical energy is not conserved.
Elastic Properties of Solids
We have seen that a spring returns to its original shape when the force compressing or stretching it is removed. In fact, all materials become distorted in some way when they are squeezed or stretched, and many of them, such as rubber, return to their original shape when the squeezing or stretching is removed. Such materials are said to be "elastic."
Concept Map: Fluids
|
|---|
You don`t have permission to comment here!
Report