Speed and Velocity

One of the most obvious features of an object in motion is how fast it is moving. If a car travels 200 meters in 10 seconds, we say its average speed is 20 meters per second, the average speed being the distance traveled divided by the time required to cover the distance:

$$\text{Average Speed}= \dfrac{\text{Distance}}{\text{Elapsed time}}$$

This equation indicates that the unit for average speed is the unit for distance divided by the unit for time, or meters per second (m/s) in SI units.

Speed is a useful idea, because it indicates how fast an object is moving. However, speed does not reveal anything about the direction of the motion. To describe both how fast an object moves and the direction of its motion, we need the vector concept of velocity.

To define the velocity of an object, we will use two concepts that we have already encountered, displacement and time. Suppose that the initial position of a car is $\vec{x_i}$ when the time is $t_i$. A little later that car arrives at the final position $\vec{x_f}$ at the time $t_f$. The difference between these times is the time required for the car to travel between the two positions. Dividing the displacement $\Delta \vec{x}$ of the car by the elapsed time $\Delta t$ gives the average velocity of the car.

$$\text{Average Velocity}= \dfrac{\text{Displacement}}{\text{Elapsed time}}$$

$$\bar{\vec{v_x}} =\dfrac{ \vec{x_f} - \vec{x_i}}{ t_f - t_i} = \dfrac{\Delta \vec{x}}{\Delta t}$$

where the subscript x indicates motion along the x axis.

This Equation indicates that the unit for average velocity is the unit for length divided by the unit for time, or meters per second (m/s) in SI units.

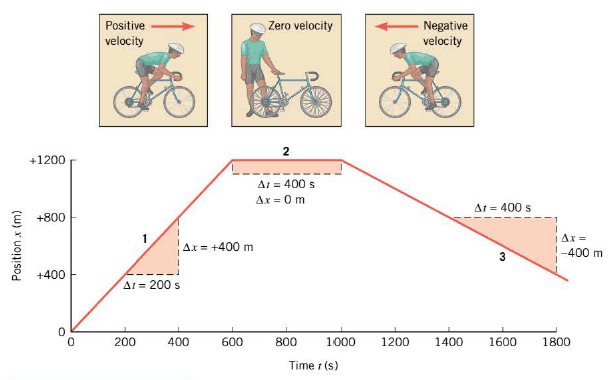
Average velocity is a vector that points in the same direction as the displacement. As with displacement, we will use plus and minus signs to indicate the two possible directions. If the displacement points in the positive direction (a particle moving in the positive x direction toward larger values of x), the average velocity is positive. Conversely, if the displacement points in the negative direction, the average velocity is negative.

hints

• In everyday usage, the terms speed and velocity are interchangeable. In physics, however, there is a clear distinction between these two quantities. Consider a marathon runner who runs a distance d of more than 40 km and yet ends up at her starting point. Her total displacement is zero, so her average velocity is zero! Nonetheless, we need to be able to quantify how fast she was running.
• The magnitude of the average velocity is not the average speed.
• Knowledge of the average velocity or average speed of a particle does not provide information about the details of the trip. You may have traveled at various speeds during the trip and you changed direction. Neither average velocity nor average speed provides information about these details.

Suppose the magnitude of your average velocity for a long trip was 20 m/s. This value, being an average, does not convey any information about how fast you were moving or the direction of the motion at any instant during the trip. Both can change from one instant to another. Surely there were times when yowr car traveled faster than 20 m/s and times when it traveled more slowly.

The instantaneous velocity $\vec{v}$ of the car indicates how fast the car moves and the direction of the motion at each instant of time. The magnitude of the instantaneous velocity is called the instantaneous speed, and it is the number (with units) indicated by the speedometer (Police give tickets based on instantaneous speed, but when calculating how long it will take to get from one place to another on a road trip, you need to use average speed).

But what does it mean to talk about how quickly something is moving if we “freeze time” and talk only about an individual instant? If the time interval has a value of zero, the displacement of the object is also zero, so the average velocity would seem to be 0/0. How do we evaluate that ratio? In the late 1600s, with the invention of calculus, scientists began to understand how to answer that question and describe an object’s motion at any moment in time.

Mathematically, the precise value of instantaneous velocity equals the limiting value (a calculus operation) of the ratio $\Delta \vec{x} / \Delta t$ as the time interval $\Delta t$ becoming extremely small, approaching zero:

$$\vec{v} = \lim_{\Delta t \to 0} \dfrac{\Delta \vec{x}}{\Delta t}$$

In calculus notation, this limit is called the derivative of x with respect to t at that point, so as $\Delta \vec{x}$ and $\Delta t$ become smaller and smaller, the ratio $\dfrac{\Delta \vec{x}}{\Delta t}$ approaches a value equal to the slope of the line tangent to the x-versus-t curve.

The instantaneous velocity at any point during a trip can be obtained by measuring the time interval $\Delta t$ for the car to travel a very small displacement $\Delta x$. If the time $\Delta t$ is small enough, the instantaneous velocity $\vec{v}$ at the point of interest is approximately equal to the average velocity computed over the interval:

$$\vec{v} \approx \bar{\vec{v}} = \dfrac{\Delta \vec{x}}{\Delta t} \;\;\; \text{(for sufficiently small $\Delta t$)}$$

hints

• For brevity, we will use the word velocity to mean "instantaneous velocity" and speed to mean "instantaneous speed."
• The magnitude of the instantaneous velocity is the instantaneous speed. In an infinitesimal time interval, the magnitude of the displacement is equal to the distance traveled by the particle.

Graphical techniques are helpful in understanding the concepts. With help from the preceding velocity defination for an object moving, the slope of the position-time graph gives the velocity.

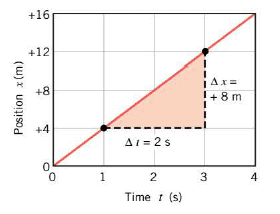
If the object is moving with constant velocity the position vs time graph will be a straight line, The slope of this line is the ratio $\Delta \vec{x} / \Delta t$, which is what we have defined as average velocity and equals the instantaneous velocity.

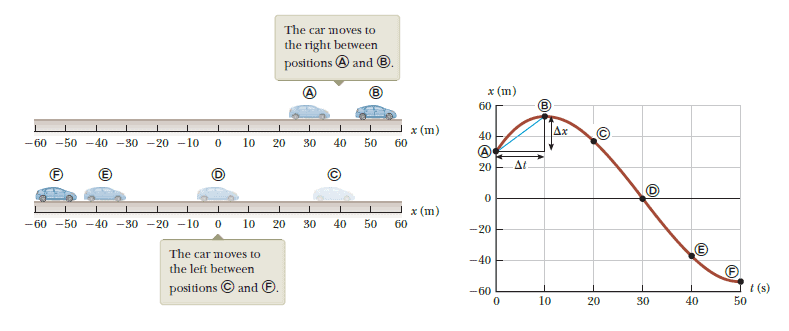
Objects rarely move with a constant velocity at all times, If the velocity of the object is constantly changing, the position vs time graph is not a straight line, but is a curve. and we can interpret average velocity geometrically by drawing a straight line between any two points on the position–time graph. The slope of this line is the average velocity. For example, the line between positions A and B in the following Figure has a slope equal to the average velocity of the car between those two times $\left( \dfrac{52 \;m - 30 \;m}{ 10 \; s - 0} = 2.2 \;\mathrm{m/s} \right)$.

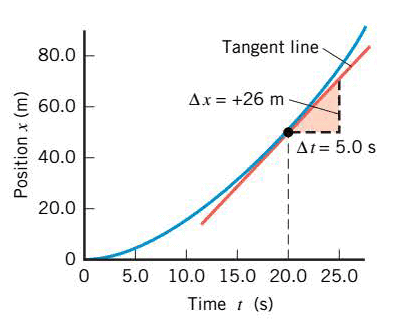
The instantaneous velocity at any instant of time can be determined by measuring the slope of the curve at that instant. Without calculus, we approximate the instantaneous velocity at a particular point by laying a straight edge along the curved line and estimating it's slope. For instance, in the following Figure a tangent line is drawn at t = 20.0 s. To determine the slope of the tangent line, a triangle is constructed using an arbitrarily chosen time interval of $\Delta t = 5.0 \;s$. The change in $x$ associated with this time interval can be read from the tangent line as $\Delta x = + 26 \;m$. Therefore, instantaneous velocity is $\left( \dfrac{+26 \;m}{ 5 \; s} = +5.2 \;\mathrm{m/s} \right)$.

This graphical result can be verified later by using Equations of Kinematics for Constant Acceleration with $v_i = 0$ and $t=20 \;s$. Note that when the slope of the position–time graph is positive, instantaneous velocity is positive and the object is moving toward larger values of x.