There are many situations in which the force acting on an object is not constant, but varies with time. For instance, a baseball being hit, and the figure illustrates approximately how the force applied to the ball by the bat changes during the time of contact. The magnitude of the force is zero at the instant $t_0$ just before the bat touches the ball. During contact, the force rises to a maximum and then returns to zero at the time $t_f$ when the ball leaves the bat. The time interval $\Delta t = t_f - t_0$ during which the bat and ball are in contact is quite short, being only a few thousandths of a second, although the maximum force can be very large, often exceeding thousands of newtons. For comparison, the graph also shows the magnitude $\vec{F}$ of the average force exerted on the ball during the time of contact.

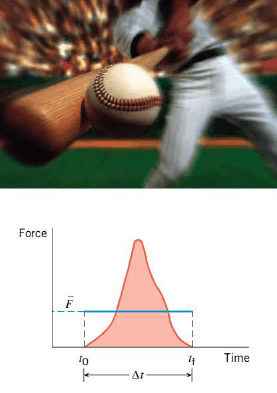
To describe how a time-varying force affects the motion of an object, we will introduce two new ideas: the impulse of a force and the linear momentum of an object. These ideas will be used with Newton's second law of motion to produce an important result known as the impulse-momentum theorem. This theorem plays a central role in describing collisions, such as that between a ball and a bat.

Momentum is the key to success in many sporting events, including baseball, football, ice hockey, and tennis. Every baseball player dreams of hitting a home run. When a player hits the ball, at the moment of collision, the ball and the bat are deformed by the collision. The resulting change in momentum determines the batter’s success.

The equality between the net force and the change in momentum per unit time is the version of the second law of motion presented originally by Newton:

$$F= ma = m \dfrac{\Delta v}{\Delta t} $$

Impulse

If a baseball is to be hit well, both the magnitude of the force and the time of contact are important. When a large average force acts on the ball for a long enough time, the ball is hit solidly. To describe such situations, we bring together the average force and the time of contact, calling the product of the two the impulse of the force.

$$\vec{J}= \bar{\vec{F}} \Delta t$$

Momentum

The product of the object’s mass and the object’s velocity is defined as the momentum of the object. Momentum is measured in kg.m/s. An object’s momentum, also known as linear momentum, is represented by the following equation:

$$p=mv $$

Impulse-Momentum Theorem

During a collision, it is often difficult to measure the net average force, so it is not easy to determine the impulse directly. On the other hand, it is usually straightforward to measure the mass and velocity of an object, so that its momentum, just after the collision and just before the collision can be found. Thus, the impulse-mon1entum theorem allows us to gain information about the impulse indirectly by measuring the change in momentum that the impulse causes. Then, armed with a knowledge of the contact time, we can evaluate the net average force.

As you learned, the angular velocity of a rotating object changes only if torque is applied to it. This is a statement of Newton’s law for rotational motion:

$$ \tau = I \alpha = I \dfrac{\Delta \omega}{\Delta t}$$

Angular Impulse

The product of a rotating object’s average torque and the time of contact is called angular impulse, and is represented by the following equation:

$$\vec{J}= \bar{\vec{\tau}} \Delta t$$

Angular Momentum

The product of a rotating object’s moment of inertia and angular velocity is called angular momentum, and is represented by the following equation:

$$L= I \omega $$

Angular Impulse-Momentum Theorem

Just as the linear momentum of an object changes when an impulse acts on it, the angular momentum of an object changes when an angular impulse acts on it. Thus, the angular impulse on the object is equal to the change in the object’s angular momentum, which is called the angular impulse-angular momentum theorem.

The total linear momentum of an isolated system remains constant (is conserved). An isolated system is one for which the vector sum of the average external forces acting on the system is zero.

Under what conditions is the momentum of the system of is conserved? The condition required to conserve the momentum of a system is that the forces involved are internal forces; that is, there are no forces acting on the system by objects outside of it. When the net external force on a system is zero, the system is described as an isolated system. No system on Earth can be said to be absolutely isolated, however, because there will always be some interactions between a system and its surroundings. Often, these interactions are small enough to be ignored when solving physics problems.

The conservation-of-momentum principle applies to a system containing any number of objects, regardless of the internal forces, provided the system is isolated. Whether the system is isolated depends on whether the vector sum of the external forces is zero.

Collisions in One Dimension

During the collision of the two balls, each one briefly exerts a force on the other. Despite the differences in sizes and velocities of the balls, the forces that they exert on each other are equal and opposite, according to Newton’s third law of motion. Because the time intervals over which the forces are exerted are the same, the impulses must be equal in magnitude but opposite in direction.

According to the impulse-momentum theorem, the change in momentum is equal to the impulse, then the sum of the momenta of the balls is the same before and after the collision. That is, the momentum gained by one ball is equal to the momentum lost by the other ball . If the system is defined as the two balls, the momentum of the system is constant, and therefore, momentum is conserved for the system.

Collisions in Two Dimensions

Up until now, you have looked at momentum in only one dimension. The law of conservation of momentum holds for all systems with no external forces. It is valid regardless of the directions of the particles before or after they interact.

Center of Mass

It is possible to speak of a kind of average location for the total mass by introducing a concept known as the center of mass (abbreviated as "cm"). With the aid of this concept, we will be able to gain additional insight into the principle of conservation of linear momentum.

Conservation of Angular Momentum

Like linear momentum, angular momentum can be conserved. The law of conservation of angular momentum states that if no net external torque acts on an object, then its angular momentum does not change.

Tops and Gyroscopes

Because of the conservation of angular momentum, the direction of rotation of a spinning object can be changed only by applying a torque. If you played with a top as a child, you may have spun it by pulling the string wrapped around its axle. When a top is vertical, there is no torque on it, and the direction of its rotation does not change. If the top is tipped, a torque tries to rotate it downward. Rather than tipping over, however, the upper end of the top revolves, or precesses slowly about the vertical axis. Because Earth is not a perfect sphere, the Sun exerts a torque on it, causing it to precess. It takes about 26,000 years for Earth’s rotational axis to go through one cycle of precession.