When algebraic operations are performed, the laws of arithmetic apply. Symbols such as $x$, $y$, and $z$ are usually used to represent unspecified quantities, called the unknowns. Physics deals with physical variables and the relations between them. Typically, variables are represented by the letters of the English and Greek alphabets. Sometimes, the relation between variables is expressed as a proportion or inverse proportion. Other times, however, it is more convenient or necessary to express the relation by means of an equation, which is governed by the rules of algebra.

One of the important aspects of physics is the search for relationships between different quantities—that is, determining how one quantity affects another.As a simple example, the ancients found that if one circle has twice the diameter of a second circle, the first also has twice the circumference. If the diameter is three times as large, the circumference is also three times as large. In other words, an increase in the diameter results in a proportional increase in the circumference. We say that the circumference is directly proportional to the diameter. This can be written in symbols as $C \propto D$ where "$\propto$" means “is proportional to”, and $C$ and $D$ refer to the circumference and diameter of a circle, respectively.

The next step is to change this proportionality to an equation, which will make it possible to link the two quantities numerically. This means inserting a proportionality constant, which in many cases is determined by measurement. The ancients found that the ratio of the circumference to the diameter of any circle was 3.1416 (to keep only the first few decimal places). This number is designated by the Greek letter $\pi$.It is the constant of proportionality for the relationship $C \propto D$. To obtain an equation, we insert $\pi$ into the proportion and change the $\propto$ to =.Thus, $C= \pi D$

Other kinds of proportionality occur as well. For example, the area of a circle is proportional to the square of its radius. That is, if the radius is doubled, the area becomes four times as large; and so on. In this case we can write $A \propto r^2$ where $A$ stands for the area and $r$ for the radius of the circle. The constant of proportionality is found to be $\pi$ again, so: $A=\pi r^2$.

Note that if $y \propto x$, then:

$$\dfrac{y_1}{y_2} = \dfrac{x_1}{x_2}$$

 

Sometimes two quantities are related in such a way that an increase in one leads to a proportional decrease in the other. This is called inverse proportion. For example, the time required to travel a given distance is inversely proportional to the speed of travel. The greater the speed, the less time it takes. We can write this inverse proportion as $time \propto \dfrac{1}{speed}$

The larger the denominator of a fraction, the lower the value of the fraction is as a whole. For example, $\frac{1}{4}$ is less than $\frac{1}{2}$.Thus, if the speed is doubled, the time is halved, which is what we want to express by this inverse proportionality relationship.

Note that if $y \propto \dfrac{1}{x}$, then:

$$\dfrac{y_1}{y_2} = \dfrac{x_2}{x_1}$$

 

If you suspect that a relationship exists between two or more quantities, you can try to determine the precise nature of this relationship by varying one of the quantities and measuring how the other varies as a result. Sometimes a given quantity is affected by two or more quantities; for instance, the acceleration of an object is related to both its mass and the applied force. In such a case, only one quantity is varied at a time, while the others are held constant.

When one quantity affects another,we often use the expression "is a function of" to indicate this dependence; for example, we say that the pressure in a tire is a function of the temperature.

Whatever kind of proportion is found to hold, it can be changed to an equality by finding the proper proportionality constant. Quantitative statements or predictions about the physical world can then be made with the equation.

We will start by supposing that you explained a phenomenon by putting it in the following equation :  

You can solve this equation for any of the variables, if you want an equation for D:    $ D = \dfrac{C \cdot B}{A}$

Although this may seem like magic, you don't have to be a "mathemagician" to do this. There are some simple steps to help you to solve an equation for any of the variables (letters that represent the element or quantity of interest).

 

You probably learned a number of rules for manipulating equations in a previous algebra course. It never hurts to remind ourselves of the rules. So let's review:

• RULE #1: you can switch all right side with all left  side of the equation, For example, if you want to solve the above equation for D, the first step is to put D on the left:
  $ A \cdot B = \dfrac{C}{D} \;\;\;\;\;\;\; \rightarrow \;\;\;\;\;\;\; \dfrac{C}{D} = A \cdot B \\$

• RULE #2: you can switch all the up with all the down of the equation, For example, the equation from Rule #1, the second step is to put D on the numerator:
  $ \dfrac{C}{D} = A \cdot B \;\;\;\;\;\;\; \rightarrow \;\;\;\;\;\;\; \dfrac{D}{C} = \dfrac{1}{A \cdot B}$
  (if there is no numerator or denominator, we can put 1 on it)
  $\\ \\$

• RULE #3: you can add, subtract, multiply and divide by anything, as long as you do the same thing to both sides of the equals sign. So to move or cancel a quantity or variable on one side of the equation, perform the "opposite" operation with it on both sides of the equation. For example, the equation from Rule #2, the last step is to get rid of C on the denominator, so multiply both sides of the equals sign by C:
  $ \dfrac{D}{C} = \dfrac{1}{A \cdot B} \;\;\;\;\;\;\; \rightarrow \;\;\;\;\;\;\; D = \dfrac{C}{A \cdot B} $

 

Example #1: Solve this equation for B

$ A \cdot B = \dfrac{C}{D} \;\;\;\;\;\;\; \rightarrow \;\;\;\;\;\;\; B = \dfrac{C}{D \cdot A} \;\;\;\;\;\;\;\; \text{(RULE #3)} $

 

Example #2: Solve this equation for D

$ A = \dfrac{C}{D^2} +E \;\; \rightarrow \;\; A - E = \dfrac{C}{D^2} \;\; \text{(RULE #3)} \;\; \rightarrow \;\; \dfrac{1}{A - E} = \dfrac{D^2}{C} \;\; \text{(RULE #2)} \\$

$\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \rightarrow \;\; \dfrac{D^2}{C} = \dfrac{1}{A - E} \;\; \text{(RULE #1)} \;\; \rightarrow \;\; D^2 = \dfrac{C}{A - E} \;\; \text{(RULE #3)} \;\; \rightarrow \;\; D = \sqrt{\dfrac{C}{A - E}} \;\; \text{(RULE #3)} $

Exercises

With help from the preceding rearranging equations rules, solve the following exercises for $x$:

• $a=\dfrac{1}{1+x}$    Answer

  Answer

  $x=\dfrac{1-a}{a}$
• $3x-5=13$    Answer

  Answer

  $x=6$
• $ax-5=bx+2$    Answer

  Answer

  $x=\dfrac{7}{a-b}$
• $\dfrac{5}{2x+6} = \dfrac{3}{4x+8}$    Answer

  Answer

  $x=-\dfrac{11}{7}$

Some of the variables in an equation typically have known values, and some do not. It is often necessary to solve the equation so that a variable whose value is unknown is expressed in terms of the known quantities. Some useful formulas for solving an equation are the following.

Fractions

$\left( \dfrac{a}{b} \right)\left( \dfrac{c}{d} \right)= \dfrac{ac}{bd} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{Multiplying} \\$

$\dfrac{a/b}{c/d} = \dfrac{ad}{bc} \;\;\;\;\;\;\;\;\;\; \dfrac{1}{1/a} = a \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{Dividing} \\$

$\dfrac{a}{b} \pm \dfrac{c}{d} = \dfrac{ad \pm bc}{bd} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{Adding}$

Factoring

$ax+ay+az = a(x+y+z) \;\;\;\;\;\;\;\; \text{common factor}$

$a^2+2ab+b^2 = (a+b)^2 \;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{perfect square}$

$a^2 - b^2 = (a+b)(a-b) \;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{differences of squares}$

 

Linear Equations

A linear equation has the general form: $y=mx+b$ where $m$ and $b$ are constants.

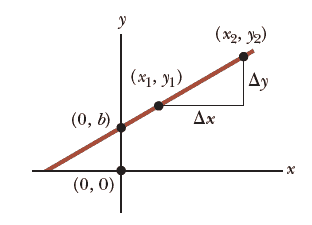This equation is referred to as linear because the graph of $y$ versus $x$ is a straight line as shown in the figure.

The constant $b$, called the y-intercept, represents the value of $y$ at which the straight line intersects the $y$ axis.

The constant $m$ is equal to the slope of the straight line. If any two points on the straight line are specified by the coordinates $(x_1, y_1)$ and $(x_2, y_2)$ as you see in the above figure, the slope of the straight line can be expressed as:

$$\text{Slope}=\dfrac{y_2 -y_1}{x_2 - x_1} = \dfrac{\Delta y}{\Delta x}$$

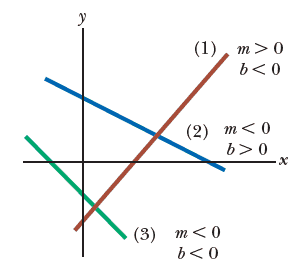Note that $m$ and $b$ can have either positive or negative values. If $m > 0$, the straight line has a positive slope. If $m < 0$ , the straight line has a negative slope. In the above figure both $m$ and $b$ are positive. Three other possible situations are shown in in the figure.

Note that proportional is a special case of linearity. If we say that $y \propto x$, means that $y=ax$, where $a$ is a constant. A graph of this proportional relationship is a straight line that passes through the origin and it's slope equals:

$$a=\dfrac{y_1}{x_1} = \dfrac{y_2}{x_2}$$

 

Simultaneous Linear Equations

When more than one variable in a single equation is unknown, additional equations are needed if solutions are to be found for all of the unknown quantities. Thus, the equation $3x + 2y = 7$ cannot be solved by itself to give unique values for both $x$ and $y$. Such an equation does not have a unique solution. For example, $(x = 0, y = 3.5)$, $(x = 5, y = -4)$, and $(x = 2, y = \frac{1}{2})$ are all solutions to this equation. However, if $x$ and $y$ also (i.e., simultaneously) obey the equation $x − 3y = 6$, then both unknowns can be found. In general, if a problem has $n$ unknowns, its solution requires $n$ equations.

There are a number of methods by which such simultaneous equations can be solved. One method is to solve one equation for $x$ in terms of $y$ and substitute the result into the other equation to obtain an expression containing only the single unknown variable $y$.

The equation $x − 3y = 6$, for instance, can be solved for $x$ by adding $3y$ to each side, with the result that $x = 6 + 3y$. The substitution of this expression for $x$ into the equation $3x + 2y = 7$ is shown below:

$$3x+2y=7 \\ 3(6+3y) +2y =7 \\ 18+9y+2y=7$$

We find, then, that $y=-1$. The value of $y$ can be substituted in either of the original equations to obtain a value for $x$ ($x=3$).

In some cases, the two pieces of information may be one equation and a condition on the solutions. For example, suppose we have the equation $m = 3n$ and the condition that $m$ and $n$ must be the smallest positive nonzero integers possible. Then, the single equation does not allow a unique solution, but the addition of the condition gives us that $n = 1$ and $m = 3$.

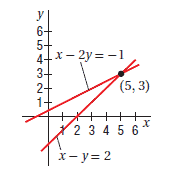Simultaneous equations can also be solved by a graphical method. If the straight lines corresponding to the two equations are plotted in a conventional coordinate system, the intersection of the two lines represents the solution.

Quadratic Equations

Equations occur in physics that include the square of a variable. Such equations are said to be quadratic in that variable, and often can be put into the following form: $ax^2+bx+c=0$ where $x$ is the unknown quantity and $a$, $b$, and $c$ are numerical factors referred to as coefficients of the equation. This equation has two roots, given by:

$$x=\dfrac{ -b \pm \sqrt{b^2 - 4ac}}{2a}$$

The $\pm$ in the formula indicates that there are two solutions. and if $b^2 \geq 4ac$, the roots are real.

 

Exercises

With help from the preceding solving equations rules, Solve the following equations:

• $x^2+5x+4=0$    Answer

  Answer

  Evaluate the root for each of the two possibilities of the sign: $x_+=-1$ and $x_- = -4$.
• $x^2+2x-3=0$    Answer

  Answer

  Evaluate the root for each of the two possibilities of the sign: $x_+=1$ and $x_- = -3$.
• $2x^2-5x+2=0$    Answer

  Answer

  Evaluate the root for each of the two possibilities of the sign: $x_+=2$ and $x_- = \dfrac{1}{2}$.
• $2x^2-4x-9=0$    Answer

  Answer

  Evaluate the root for each of the two possibilities of the sign: $x_+= 1+ \dfrac{\sqrt{22}}{2}$ and $x_- = 1- \dfrac{\sqrt{22}}{2}$.
• Find the slopes of the straight lines: $(\text{a})\; y=5x+3 \;\;\;$ $(\text{b})\; y=-2x+4\;\;\;$ $(\text{c})\; y=-3x-6$     Answer

  Answer

  $(\text{a})\; 5\;\;\;$ $(\text{b})\; -2\;\;\;$ $(\text{c})\; -3$.
• Find the slopes of the straight lines that pass through the following points: $(\text{a})\; (0,-4)$ and $(4,2) \;\;\;$ $(\text{b})\; (0,0)$ and $(2,-5) \;\;\;$ $(\text{c})\; (-5,2)$ and $(4,-2)$     Answer

  Answer

  $(\text{a})\; \dfrac{3}{2}\;\;\;$ $(\text{b}) \; -\dfrac{5}{2}\;\;\;$ $(\text{c})\; -\dfrac{4}{9}$.
• Solve the following pairs of simultaneous equations involving two unknowns: $x+y=8 \;\;\;\;\;\;$ $x-y=2$     Answer

  Answer

  $x=5,y=3$.
• Solve the following pairs of simultaneous equations involving two unknowns: $98+T=10a \;\;\;\;\;\;$ $T-49=5a$     Answer

  Answer

  $T=65,a=3.27$.
• Solve the following pairs of simultaneous equations involving two unknowns: $6x+2y=6 \;\;\;\;\;\;$ $8x-4y=28$     Answer

  Answer

  $x=2,y=-3$.