In various branches of science, it is sometimes necessary to use the basic tools of calculus, invented by Newton, to describe physical phenomena. The use of calculus is fundamental in the treatment of various problems in Newtonian mechanics, electricity, and magnetism.

First, a function must be specified that relates one variable to another (e.g., position as a function of time).

Suppose one of the variables is called $y$ (the dependent variable), and the other $x$ (the independent variable). We might have a function relationship such as:

$y(x) = ax^3 + bx^2 + cx + d$

If $a, b, c$ and $d$ are specified constants, $y$ can be calculated for any value of $x$.

We usually deal with continuous functions, that is, those for which $y$ varies “smoothly” with $x$.

 

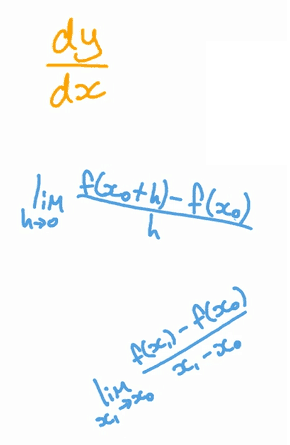
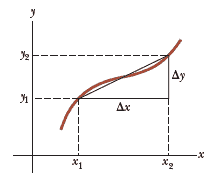The derivative of $y$ with respect to $x$ is defined as the limit as $\Delta x$ approaches zero of the slopes of chords drawn between two points on the $y$ versus $x$ curve.

Mathematically, we write this definition as:

$$ \dfrac{dy}{dx} = \lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \dfrac{y(x+ \Delta x) - y(x)}{\Delta x}$$

where $\Delta y = y_2 - y_1$ and $\Delta x = x_2 - x_1$

But the concept of limits is very complicated, and we don’t want to introduce it without really explaining it. So, we will introduce the derivative as the slope of the linear approximation.

Let’s better define the slope! In our case, the slope is the ratio of the variation of the value of linear approximation of the function by the variation of the argument of the function. Now, to compute the slope, we have to consider a variation of $x$. Overall, a variation of $x$ of $\Delta x$ has induced a variation of $y$ of $\Delta y$. The slope is the ratio of the effect of the variation by the variation. Thus, the slope of the linear approximation is $\dfrac{\Delta y}{\Delta x}$. So the unit of this slope is a $\Delta y$ per $\Delta x$. It means that if we vary $x$ value by 1, then $y$ value will increase by the slope value.

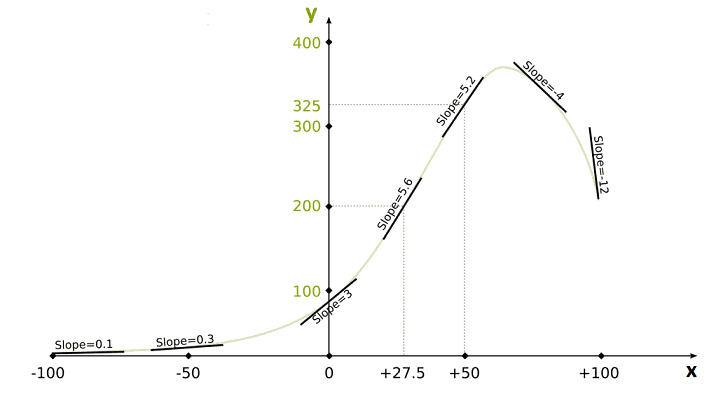
The slope of the linear approximation of a function is called the derivative of the function. But it’s important to notice that the derivative depends on the $x$ value where we compute it, because the linear approximation depends on this $x$ value. The following figure shows linear approximations for different $x$ values:

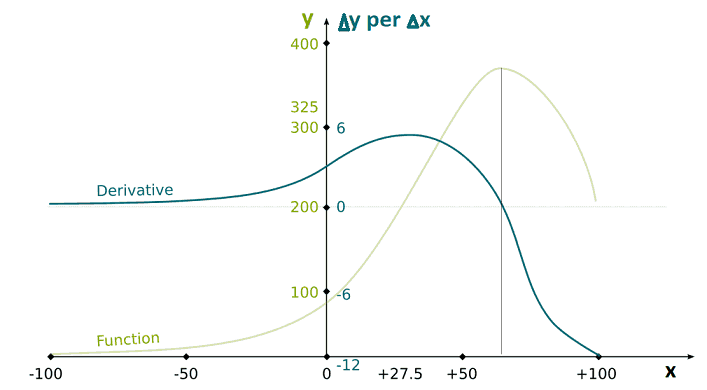
This sounds like a function, doesn’t it? The derivative is actually the function that maps $x$ values with slopes of the linear approximations. And we can draw this function, just like we drew our original function. In fact, one usual and nice way to do this is to draw the function on the same graph, but with a different vertical scale. Indeed, for instance, the unit must correspond to the unit of the derivative, as displayed in blue in the following figure:

Now, if your function has an explicit form, like $y(x) = ax^3 + bx^2 + cx + d$, then there are formulas to obtain an explicit form of the derivative.

As you can see in the previous figures, if the slope of the linear approximation is positive, then this means that the function is increasing indeed, the function is locally increasing if and only if its derivative is positive. Similarly, the function is locally decreasing if and only if its derivative is negative. If a point is a maximum or a minimum, then its derivative can neither be positive nor negative: the derivative is therefore nil.

A useful expression to remember when $y(x) = ax^n$ where $a$ is a constant and $n$ is any positive or negative number (integer or fraction), is:

$$\dfrac{dy}{dx} = n a x^{n-1}$$

If $y(x)$ is a polynomial or algebraic function of $x$, we apply this Equation to each term in the polynomial and take $\dfrac{d \text{[constant]}}{dx} = 0$.

Examples:

$\dfrac{d}{dx} \left( a \right) = 0 \\$ $\dfrac{d}{dx} \left( a x^n \right) = nax^{n-1} \\$ $\dfrac{d}{dx} \left( e^{ax} \right) = a e^{ax} \\$ $\dfrac{d}{dx} \left( \sin ax \right) = a \cos ax \\$ $\dfrac{d}{dx} \left( \cos ax \right) = - a \sin ax \\$ $\dfrac{d}{dx} \left( \tan ax \right) = a \sec^2 ax \\$ $\dfrac{d}{dx} \left( \cot ax \right) = -a \csc^2 ax \\$ $\dfrac{d}{dx} \left( \sec x \right) = \tan x \sec x \\$ $\dfrac{d}{dx} \left( \csc x \right) = - \cot x \csc x \\$ $\dfrac{d}{dx} \left( \ln ax \right) = \dfrac{1}{x} \\$ $\dfrac{d}{dx} \left( \sin^{-1} ax \right) = \dfrac{a}{ \sqrt{1-a^2 x^2}} \\$ $\dfrac{d}{dx} \left( \cos^{-1} ax \right) = \dfrac{-a}{ \sqrt{1-a^2 x^2}} \\$ $\dfrac{d}{dx} \left( \tan^{-1} ax \right) = \dfrac{a}{1+a^2 x^2} $

• Derivative of the product of two functions

  If a function $f(x)$ is given by the product of two functions—say, $g(x)$ and $h(x)$ —the derivative of $f(x)$ is defined as:

  $$\dfrac{d}{dx} f(x) = \dfrac{d}{dx} [g(x) h(x)] = g \dfrac{dh}{dx} + h \dfrac{dg}{dx}$$

• Derivative of the sum of two functions

  If a function $f(x)$ is equal to the sum of two functions, the derivative of the sum is equal to the sum of the derivatives:

  $$\dfrac{d}{dx} f(x) = \dfrac{d}{dx} [g(x) + h(x)] = \dfrac{dg}{dx} + \dfrac{dh}{dx}$$

• Chain rule of differential calculus

  If $y = f(x)$ and $x = g(z)$, then $\dfrac{dy}{dz}$ can be written as the product of two derivatives:

  $$\dfrac{dy}{dz} = \dfrac{dy}{dx} \dfrac{dx}{dz} $$

• The second derivative

  The second derivative of $y$ with respect to $x$ is defined as the derivative of the function $\dfrac{dy}{dx}$ (the derivative of the derivative). It is usually written as:

  $$\dfrac{d^2 y}{dx^2} = \dfrac{d}{dx} \left( \dfrac{dy}{dx} \right)$$