When we write $10^4$ we mean that you multiply 10 by itself four times: $10^4 = 10 \times 10 \times 10 \times 10 = 10000$.
The superscript 4 is called an exponent, and 10 is said to be raised to the fourth power. Any number or symbol can be raised to a power. Special names are used when the exponent is 2 ($B^2$ is “a squared”) or 3 ($B^3$ is “a cubed”). For any other power, we say $B^n$ is “B to the nth power.”
If the exponent is 1, it is usually dropped: $B^1 = B$ since no multiplication is involved.
Logarithms are closely related to exponents. note that it is possible to express any number $y$ as another number $B$ raised to the exponent $x$, the exponent $x$ is called the logarithm of the number $y$ to the base $B$:
$$\text{if} \;\;\;\; y=B^x , \;\;\;\;\text{then}\;\;\;\; x=\log_{B} y$$
In practice,, one of two choices for the base number is usually used. If $B = 10$, the logarithm is known as the common logarithm, for which the notation “$\log$” applies:
$$\text{if} \;\;\;\; y=10^x , \;\;\;\text{then}\;\;\;\; x=\log y$$
If $B = e = 2.718 …$ (natural number), the logarithm is referred to as the natural logarithm, and the notation “$\ln$” is used:
$$\text{if} \;\;\;\; y=e^x , \;\;\;\;\text{then}\;\;\;\; x=\ln y$$
For any number $y$, the two types of logarithms are related by:
$$\ln y = 2.3026 \log y$$
Both kinds of logarithms are often given on calculators.
Rules of Exponents
$x^n x^m = x^{n+m} \;\;\;\;\;\;\;\;\;\;\;\;\;\;$ When multipling the powers of a given quantity
$x^0 = 1 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ A power that is zero $(x^n \times x^{-n} = x^0=1)$
$\dfrac{x^n}{x^m} = x^{n-m} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ When dividing the powers of a given quantity
$x^{\frac{1}{n}} = \sqrt[n]{x} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ A power that is a fraction
$\left( x^n \right)^m = x^{nm} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;$ An exponent raised to another power
Exercises
With help from the preceding exponents rules, Verify the following equations:
- $3^2 \times 3^3 =243 \\$
- $x^5 \times x^{-8} =x^{-3} \\$
- $\dfrac{x^{10}}{x^{-5}} =x^{15} \\$
- $x^{\frac{1}{3}} =1.709976 \;\; \text{(Use your calculator)} \\ $
- $60^{\frac{1}{4}} =2.783158 \;\; \text{(Use your calculator)} \\$
- $\left( x^4 \right)^3 =x^{12}$
Rules of Logarithms
$\log (ab) = \log a + \log b \\$
$\log \left( \dfrac{a}{b} \right) = \log a - \log b \\$
$\log \left( a^n \right) = n \log a$
$\ln e = 1 \\$
$\ln e^a = a \\$
$\ln \left( \dfrac{1}{a} \right) = - \ln a $
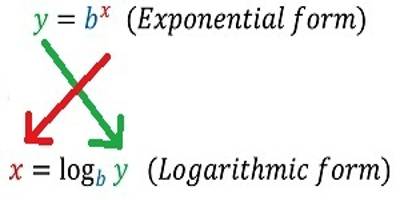
You don`t have permission to comment here!
Report