We review here a number of theorems involving angles and geometric shapes that are useful in physics.
Equal angles
Two angles are equal if any of the following conditions are true:
-
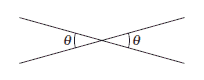
They are vertical angles.
-
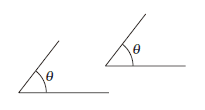
Their sides are parallel (the left side of one is parallel to the left side of the other, and the right side of one is parallel to the right side of the other).
-
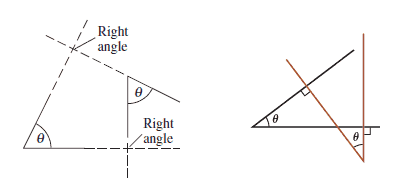
Their sides are mutually prependicular (the left side of one is perpendicular to the left side of the other, and the right sides are likewise perpendicular).
Radian measure
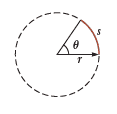
The arc length $s$ of a circular arc is proportional to the radius $r$ for a fixed value of $\theta$ (in radians), the angle $\theta$ in radians is the ratio of the arc length $s$ to the radius $r$ of the circle:
$$\text{The arc length that spans angel is:} \;\; s= r \theta $$
$$\text{The angle in radians is defined as:} \;\; \theta=\dfrac{s}{r}$$
A full circle is represented by 360 degrees ($360^o$) or by $2 \pi$ radians ($2 \pi \;\mathrm{rad}$):
$$2 \pi \;\mathrm{rad} = 360^o$$
As such, the following conversions can be used:
$$[\text{angle}\; (^o)] = \dfrac{180}{\pi} \;[\text{angle}\; (\mathrm{rad})]$$
$$[\text{angle}\; (\mathrm{rad})] = \dfrac{\pi}{180} \;[\text{angle}\; (^o)]$$
Circumferences, Areas, Volumes of some common shapes
 |
$$\text{Area}=lw$$ |
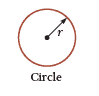 |
$\text{Circumference}=2 \pi r$ $\text{Area}=\pi r^2$ |
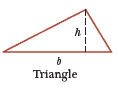 |
$\text{Area}=\frac{1}{2} bh$ |
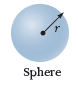 |
$\text{Surface Area}=4 \pi r^2$ $\text{Volume}=\dfrac{4 \pi r^3}{3}$ |
 |
$\text{Lateral Surface Area}=2 \pi rl$ $\text{Volume}=\pi r^2 l$ |
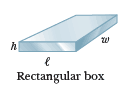 |
$\text{Surface Area}=2 (lh + lw+ hw)$ $\text{Volume}=lwh$ |
Shapes Equations
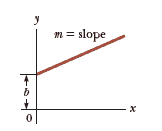 |
||
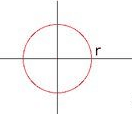 |
||
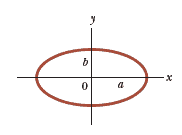 |
||
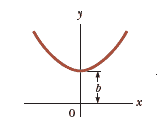 |
||
 |

You don`t have permission to comment here!
Report