Integral Calculus
As an example, the result of differentiating the function $y(x) = ax^3 +bx+c $ was:
$$f(x) = \dfrac{dy}{dx} = 3 ax^3 +b$$We can write this Equation as $dy= f(x) dx = (3 ax^3 +b) dx$ and obtain $y(x)$ by “summing” over all values of $x$. Mathematically, we write this inverse operation as:
$$y(x) = \int f(x) dx = \int (3 ax^3 +b) dx = ax^3+bx+c$$where $c$ is a constant of the integration.
Indefinite and Definite integrals
The above example of integral is called an indefinite integral because its value depends on the choice of $c$. A general indefinite integral $I(x)$ is defined as:
$$I(x) = \int f(x) dx$$where $f (x)$ is called the integrand and $f(x) = \dfrac{dI(x)}{dx}$.
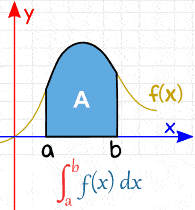
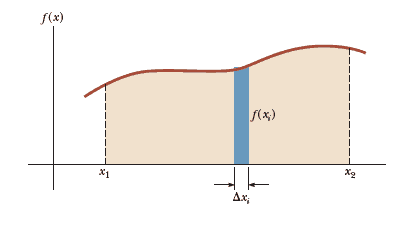 For a general continuous function $f(x)$, the integral can be interpreted geometrically as the area under the curve bounded by $f(x)$ and the $x$ axis, between two specified values of $x$, say, $x_1$ and $x_2$.
For a general continuous function $f(x)$, the integral can be interpreted geometrically as the area under the curve bounded by $f(x)$ and the $x$ axis, between two specified values of $x$, say, $x_1$ and $x_2$.
The area of the blue element in the figure is approximately $f(x_i)$ $\Delta x_i$. If we sum all these area elements between $x_1$ and $x_2$ and take the limit of this sum as $\Delta x_i \to 0$, we obtain the true area under the curve bounded by $f(x)$ and the $x$ axis, between the limits $x_1$ and $x_2$:
$$\text{Area}= \lim_{\Delta x_i \to 0} \sum_{i} f(x_i) \Delta x_i =\int^{x_2}_{x_1} f(x) dx $$Integrals of the type defined by the above Equation are called definite integrals.
One common integral that arises in practical situations has the form:
$\int x^n dx = \dfrac{x^{n+1}}{n+1} + c \;\;\;\;\;\;\;\;\; (n \neq -1)$This result is obvious, being that differentiation of the right-hand side with respect to $x$ gives $f(x)= x^n$ directly.
If the limits of the integration are known, this integral becomes a definite integral and is written:
$\int_{x_1}^{x_2} x^n dx = \left.\begin{matrix} \dfrac{x^{n+1}}{n+1} \end{matrix}\right|_{x_1}^{x_2} = \dfrac{x_2^{n+1} - x_1^{n+1}}{n+1} \;\;\;\;\;\;\;\;\; (n \neq -1)$Useful indefinite integrals
Useful definite integrals
Exercises
With help from the preceding integration rules, evaluate the integral:
Online Calculators: Indefinite integral
|
Online Calculators: Definite integral
|
|---|
Partial Integration
Sometimes it is useful to apply the method of partial integration (also called “integrating by parts”) to evaluate certain integrals. This method uses the property:
$$\int u dv = uv - \int v du$$where $u$ and $v$ are carefully chosen so as to reduce a complex integral to a simpler one.
In many cases, several reductions have to be made. Consider the function:
$I(x) = \int x^2 e^x dx$which can be evaluated by integrating by parts twice. First, if we choose $u = x^2$, $v = e^x$, we obtain:
$\int x^2 e^x dx = \int x^2 d(e^x) = x^2 e^x - 2 \int e^x x dx + c_1$Now, in the second term, choose $u=x$, $v=e^x$, which gives:
$\int x^2 e^x dx = x^2 e^x - 2 x e^x + 2 \int e^x dx + c_1 \\$ $\int x^2 e^x dx = x^2 e^x - 2 x e^x + 2 e^x + c_2$The Perfect Differential
Another useful method to remember is that of the perfect differential, in which we look for a change of variable such that the differential of the function is the differential of the independent variable appearing in the integrand. For example, consider the integral:
$I(x) = \int \cos^2 x \sin x dx$This integral becomes easy to evaluate if we rewrite the differential as $d (\cos x) = -\sin x dx$. The integral then becomes:
$\int \cos^2 x \sin x dx = -\int \cos^2 x d(\cos x)$If we now change variables, letting $y = \cos x$, we obtain:
$\int \cos^2 x \sin x dx = - \int y^2 dy = -\dfrac{y^3}{3} + c = - \dfrac{\cos^3 x}{3} +c$
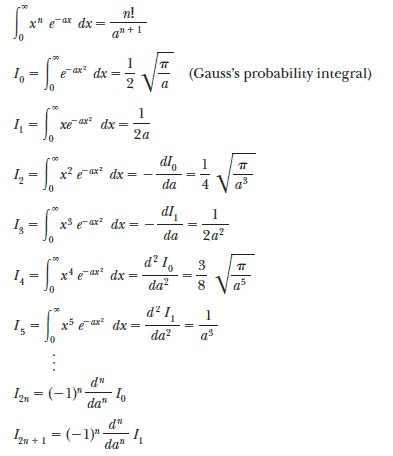
You don`t have permission to comment here!
Report