Scientific Notation

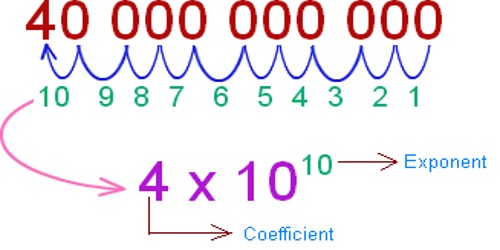
Many quantities used by scientists often have very large or very small values. The speed of light, for example, is about 300 000 000 m/s and the ink required to make the dot over an i has a mass of about 0.000 000 001 kg. Obviously, it is very cumbersome to read, write, and keep track of the numbers of zeros in such quantities. We avoid this problem by using a method incorporating powers of the number 10.

Positive exponents:

The number of zeros determines the power to which 10 is raised, or the exponent of 10, as the value of the positive exponent equals the number of places the decimal point must be moved to be to the left of the first nonzero digit (in these cases, the digit 3). For example, the speed of light, 300 000 000 m/s, can be expressed as $3 \times 10^8 \;\mathrm{m/s}$. In this case, the exponent of 10 is 8:

Negative exponents:

The value of the negative exponent equals the number of places the decimal point must be moved to be to the right of the first nonzero digit (in these cases, the digit 1). For example, the ink mass of about 0.000 000 001 kg, can be expressed as $1 \times 10^{-9} \;\mathrm{kg}$. In this case, the exponent of 10 is -9:

Scientific Notation Converter

Exercises

With help from the preceding scientific notation rules, verify the answers to the following examples:

• $86 400$    Answer

  Answer

  $86 400= 8.64 \times 10^4$
• $9 816 762.5$    Answer

  Answer

  $9 816 762.5 = 9.816 762 5 \times 10^6$
• $0.000 000 039 8$    Answer

  Answer

  $0.000 000 039 8 = 3.98 \times 10^{-8}$
• $(4.0 \times 10^8)(9.0 \times 10^9)$    Answer

  Answer

  $(4.0 \times 10^8)(9.0 \times 10^9) = 3.6 \times 10^{18}$
• $(3.0 \times 10^7)(6.0 \times 10^{-12})$    Answer

  Answer

  $(3.0 \times 10^7)(6.0 \times 10^{-12}) = 1.8 \times 10^{-4}$
• $\dfrac{75 \times 10^{-11}}{5.0 \times 10^{-3}}$    Answer

  Answer

  $\dfrac{75 \times 10^{-11}}{5.0 \times 10^{-3}} = 1.5 \times 10^{-7}$
• $\dfrac{(3 \times 10^6)(8 \times 10^{-2})}{(2 \times 10^{17})(6 \times 10^{5})}$     Answer

  Answer

  $\dfrac{(3 \times 10^6)(8 \times 10^{-2})}{(2 \times 10^{17})(6 \times 10^{5})} = 2 \times 10^{-18}$

Significant figures

sig figs are the number of digits in a measurement that are reliable and actually provide information, and are a method of tracking measurement precision, in a way that allows you to propagate your precision limits throughout your calculation.

Significant figures Calculator

hints

• Most of the numerical problems yield answers having three significant figures.
• When carrying out estimation calculations, we shall typically work with a single significant figure.
• When solving problems, it is very useful to perform the solution completely in algebraic form and wait until the very end to enter numerical values into the final symbolic expression. This method will save many calculator keystrokes, especially if some quantities cancel so that you never have to enter their values into your calculator! In addition, you will only need to round once, on the final result

Exercises

With help from the preceding sig figs rules, how many significant figures are in the following numbers:

• $78.9 \pm 0.2$    Answer

  Answer

  The $\pm 0.2$ following the 78.9 expresses uncertainty in the last digit. Therefore, there are three significant figures in $78.9 \pm 0.2$.
• $3.788 \times 10^9$    Answer

  Answer

  Scientific notation is often used to remove the ambiguity of the number of significant figures in a number. Therefore, all the digits in 3.788 are significant, and $3.788 \times 10^9$ has four significant figures.
• $2.46 \times 10^{-6}$    Answer

  Answer

  Scientific notation is often used to remove the ambiguity of the number of significant figures in a number. Therefore, all the digits in 2.46 are significant, and $2.46 \times 10^{-9}$ has three significant figures.
• $0.0053$    Answer

  Answer

  Zeros used to position the decimal point are not significant. Therefore 0.0053 has two significant figures.
• A carpet is to be installed in a rectangular room whose length is measured to be 12.71 m and whose width is measured to be 3.46 m. Find the area of the room.    Answer

  Answer

  If you multiply 12.71 m by 3.46 m on your calculator, you will see an answer of 43.9766 m$^2$. How many of these numbers should you claim? Our rule of thumb for multiplication tells us that you can claim only the number of significant figures in your answer as are present in the measured quantity having the lowest number of significant figures. In this example, the lowest number of significant figures is three in 3.46 m, so we should express our final answer as 44.0 m$^2$.
• the sum of the measured values 756, 37.2, 0.83, and 2    Answer

  Answer

  756 + 37.2 + 0.83 + 2 = 796.03 = 796, since the number with the fewest decimal places is 2.
• the product $0.003 2 \times 356.3$    Answer

  Answer

  $0.0032 (2 s.f) \times 356.3 (4 s.f) = 1.14016 =$ 1.1 (2 s.f)