Skip to main content
Log in Register

      

yjetdrsetghgtu

By definition, a right triangle is a triangle containing a $90^o$ angle.

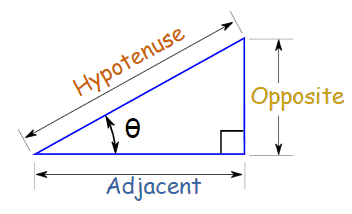
Trigonometric functions for any angle are defined by constructing a right triangle about that angle as shown in the figure to the right,

opp and adj are the lengths of the sides opposite and adjacent to the angle $\theta$ and hyp is the length of the hypotenuse.

 

Basic trigonometric functions

$\sin \theta = \dfrac{\text{opp}}{\text{hyp}}$
$\theta = \sin^{-1} \dfrac{\text{opp}}{\text{hyp}}$
$\cos \theta = \dfrac{\text{adj}}{\text{hyp}}$
$\theta = \cos^{-1} \dfrac{\text{adj}}{\text{hyp}}$
$\tan \theta = \dfrac{\text{opp}}{\text{adj}} = \dfrac{\sin \theta}{\cos \theta}$
$\theta = \tan^{-1} \dfrac{\text{opp}}{\text{adj}}$

The Pythagorean theorem provides the following relationship among the sides of a right triangle:

$\text{hyp}^2 = \text{adj}^2 + \text{opp}^2$
$\text{hyp} = \sqrt{\text{adj}^2 + \text{opp}^2}$

 

Show Videos Hide Videos

Some Trigonometric Identities

From the preceding definitions and the Pythagorean theorem, it follows that:

$\sin^2 \theta + \cos^2 \theta = 1$

The cosecant, secant, and cotangent functions are defined by:

$\csc \theta = \dfrac{1}{\sin \theta}$
$\sec \theta = \dfrac{1}{\cos \theta}$
$\cot \theta = \dfrac{1}{\tan \theta}$

The following are some useful identities among the trigonometric functions:

$\sin 2\theta = 2 \sin \theta \cos \theta$
$\cos 2\theta = \cos^2 \theta - \sin^2 \theta$
$\tan 2 \theta = \dfrac{2 \tan \theta }{1- \tan^2 \theta}$
$\sin \dfrac{\theta}{2} = \sqrt{ \dfrac{1-\cos \theta}{2} }$
$\cos \dfrac{\theta}{2} = \sqrt{ \dfrac{1+\cos \theta}{2} }$
$\tan \dfrac{\theta}{2} = \sqrt{ \dfrac{1-\cos \theta}{1+ \cos \theta} }$
$\sin^2 \dfrac{\theta}{2} = \dfrac{1- \cos \theta}{2}$
$\cos^2 \dfrac{\theta}{2} = \dfrac{1+ \cos \theta}{2}$
  
$\sin(A \pm B) = \sin A \cos B \pm \cos A \sin B$
$\cos(A \pm B) = \cos A \cos B \mp \sin A \sin B$
$\tan(A \pm B) = \dfrac{ \tan A \pm \tan B}{1 \mp \tan A \tan B}$
$\sin A \pm \sin B = 2 \sin \left( \dfrac{A \pm B}{2} \right) \cos \left( \dfrac{A \mp B}{2} \right)$
$\cos A + \cos B = 2 \cos \left( \dfrac{A + B}{2} \right) \cos \left( \dfrac{A - B}{2} \right)$
$\cos A - \cos B = 2 \sin \left( \dfrac{A + B}{2} \right) \sin \left( \dfrac{B - A}{2} \right)$

Some properties of trigonometric functions are the following:

$\sin (- \theta) =- \sin \theta$
$\cos ( - \theta) = \cos \theta$
$\tan ( - \theta) = -\tan \theta$
$\sin (90^o - \theta) = \cos \theta$
$\cos (90^o - \theta) = \sin \theta$
  
$\sin (180^o - \theta) = \sin \theta$
$\cos (180^o - \theta) = -\cos \theta$
  

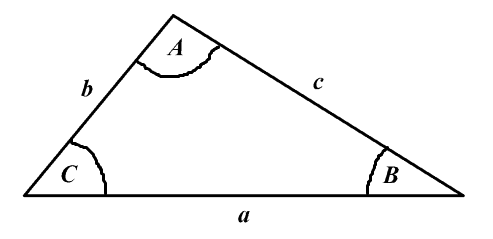
For any triangle

A right triangle has one angle that is 90°. An isosceles triangle has two sides that are equal. An equilateral triangle has three sides that are equal. Each angle of an equilateral triangle is 60°.

tri3

  • The sum of the angles of any triangle is 180°: $ \;\;\;\;\; A+B+C = 180^o $

  • Two triangles are similar if two of their angles are equal. The corresponding sides of similar triangles are proportional to each other: $ \;\;\;\;\; \dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2}$

  • The law of cosines and the law of sines apply to any triangle, not just a right triangle, and they relate the angles and the lengths of the sides:

    $\dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c} \;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{law of sines} \\ $

    $c^2 = a^2 + b^2 -2 ab \cos C \;\;\;\;\;\;\;\;\;\;\;\;\;\; \text{law of cosines}$

 

 

Exercises

With help from the preceding trigonometry rules, try to solve the following exambles:

  • In a certain right triangle, the two sides that are perpendicular to each other are 5.00 m and 7.00 m long. What is the length of the third side?     Answer

    Answer

    8.60 m.
  • In a certain right triangle, the two sides that are perpendicular to each other are 3.00 m and 4.00 m long. What are the angels of the triangle?     Answer

    Answer

    $90^o,53.1^o \;\text{and} \; 36.9^o$.
  • A right triangle has a hypotenuse of length 3.0 m, and one of its angles is $30^o$. (a) What is the length of the side opposite the $30^o$ angle? (b) What is the side adjacent to the $30^o$ angle?     Answer

    Answer

    (a) 1.5 m (b) 2.6 m.

 

You don`t have permission to comment here!