Unit Conversions
The first step toward ensuring accuracy and reproducibility is defining the units in which the measurements are made.
Units of Measurement
Usualy, we emphasize the system of units known as SI units, which stands for the French phrase “Le Système International d'Unités.” By international agreement, this system employs the meter (m) as the unit of length, the kilogram (kg) as the unit of mass, and the second (s) as the unit of time.
The units for length, mass, and time, along with a few other units that will arise later, are regarded as base SI units. The word “base” refers to the fact that these units are used along with various laws to define additional units for other important physical quantities, such as force and energy. The units for such other physical quantities are referred to as derived units, since they are combinations of the base units. Derived units will be introduced from time to time, as they arise naturally along with the related physical laws.
SI base units
|
|
|
|||
| Name | Typical symbol | Name | Symbol | |
| time | t | second | s | |
| length | l, x, r, etc. | metre | m | |
| mass | m | kilogram | kg | |
| electric current | I, i | ampere | A | |
| thermodynamic temperature | T | kelvin | K | |
| amount of substance | n | mole | mol | |
| luminous intensity | Iv | candela | cd | |
SI prefixes (convert within the SI system)
The value of a quantity in terms of base or derived units is sometimes a very large or very small number. In such cases, it is convenient to introduce larger or smaller units that are related to the normal units by multiples of ten. In the SI system there is a standard Prefixes Used to Denote Multiples of Ten. For example, 1000 or $10^3$ meters are referred to as 1 kilometer (km), and 0.001 or $10^{−3}$ meter is called 1 millimeter (mm). Similarly, 1000 grams and 0.001 gram are referred to as 1 kilogram (kg) and 1 milligram (mg), respectively.
SI prefixes
| Factor | Name | Symbol | Multiplying Factor |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
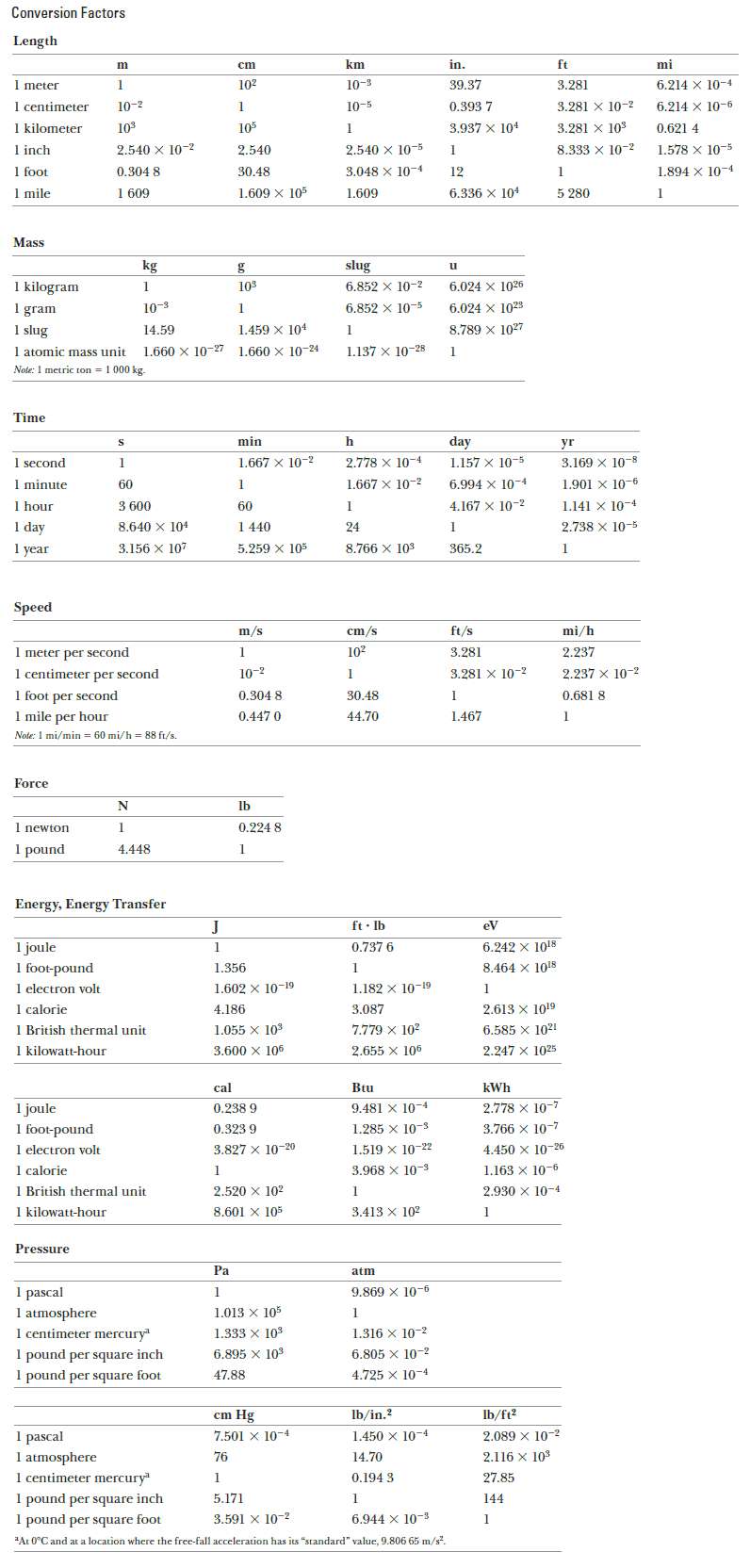
Conversion factors (convert between SI and another measurement system)
Since any quantity, such as length, can be measured in several different units, it is important to know how to convert from one unit to another. For instance, the foot can be used to express the distance between two marks. There are 3.281 feet in one meter, and this number can be used to convert from meters to feet. For example, suppose we wish to convert 15.0 feet to meters, we find that:
$15.0 \;\mathrm{ft} = (15.0 \; \require{cancel} \cancel{\mathrm{ft}}) \left( \dfrac{1 \;\mathrm{m}}{3.281 \; \cancel{\mathrm{ft}}} \right) = 4.57 \;\mathrm{m}$
where the ratio in parentheses is equal to 1. We express 1 as 1 m/3.281 ft (rather than 3.281 ft/1 m) so that the unit “feet” in the denominator cancels with the unit in the original quantity. The remaining unit is the meter, our desired result.
You see that, when converting between units, we write down the units explicitly in the calculations and treat them like any algebraic quantity that can cancel each other. In particular, we take advantage of the following algebraic fact: Multiplying or dividing an equation by a factor of 1 does not alter an equation.
Conversion factors
hints
- When performing calculations with numerical values, include the units for every quantity and carry the units through the entire calculation. Avoid the temptation to drop the units early and then attach the expected units once you have an answer. By including the units in every step, you can detect errors if the units for the answer turn out to be incorrect.
- In any conversion, if the units do not combine algebraically to give the desired result, the conversion has not been carried out properly.
- In particular, remember that only quantities with the same units can be added or subtracted.
Exercises
With help from the preceding unit conversions rules, solve the following examples:
- On an interstate highway in a rural region of Wyoming, a car is traveling at a speed of 38.0 m/s. Is the driver exceeding the speed limit of 75.0 mi/h? Answer
- A student sees a newspaper ad for an apartment that has 1330 square feet ($\mathrm{ft^2}$) of floor space. How many square meters of area are there? Answer
Online Converter: Distance and Length
|
Online Converter: Weight and Mass
|
Online Converter: Time
|
|
|---|---|---|---|
Online Converter: Area
|
Online Converter: Volume
|
Online Converter: Speed
|
Online Converter: Temperature
|
You don`t have permission to comment here!
Report