Vectors and Coordinate Systems

Some common scalars are temperature (e.g., 20°C) and mass (e.g., 85 kg).

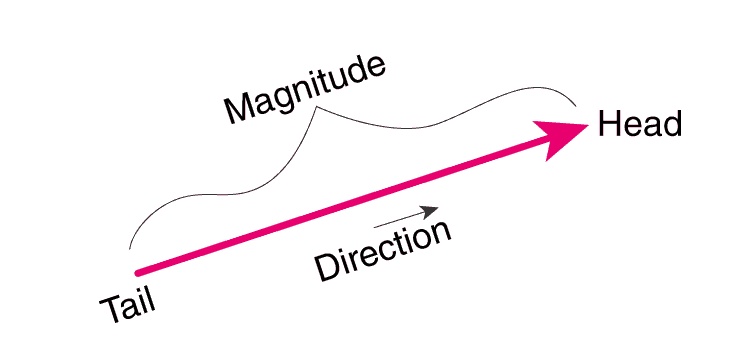
While many quantities in physics are scalars, there are also many that are not, and for these quantities the magnitude tells only part of the story. A vector quantity is completely specified by a number with an appropriate unit (the magnitude of the vector) plus a direction.

Vectors are geometric representations of magnitude and direction and can be expressed as arrows in two or three dimensions.

Many aspects of physics involve a description of a location in space.

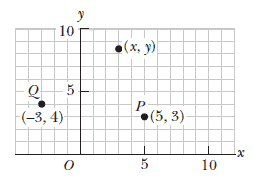In two dimensions, this description is accomplished with the use of the Cartesian coordinate system, in which perpendicular axes intersect at a point defined as the origin $O$ . Cartesian coordinates of a point in space, representing the $x$ and $y$ values of the point, and expressed as $(x, y)$, are also called rectangular coordinates.

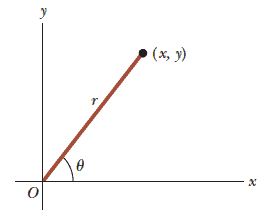Sometimes it is more convenient to represent a point in a plane by its plane polar coordinates $(r, \theta)$. In this polar coordinate system, $r$ is the distance from the origin to the point having Cartesian coordinates $(x, y)$ and $\theta$ is the angle between a fixed axis and a line drawn from the origin to the point. The fixed axis is often the positive $x$ axis, and $\theta$ is usually measured counterclockwise from it.

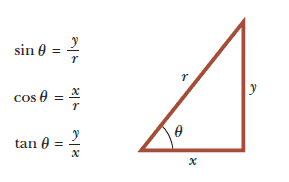To relate $(x, y)$ to $(r, \theta)$, starting with the plane polar coordinates of any point, we can obtain the Cartesian coordinates from the right triangle in the figure:

by using the equations:

$$x=r \cos \theta \;\;\;\;\;\;\;\;\;\; y=r \sin \theta$$

Conversely, if we know the Cartesian coordinates, the polar coordinates are given by:

$$\tan \theta = \dfrac{y}{x} \;\;\;\;\;\;\;\;\;\;\; r=\sqrt{x^2 +y^2}$$

We use a boldface letter with an arrow over the letter, such as $\vec{A}$ , to represent a vector.

The magnitude of the vector $\vec{A}$ is written as $\left| \vec{A} \right|$. The magnitude of a vector has physical units, such as meters for displacement or meters per second for velocity. The magnitude of a vector is always a positive number.

We graphically represent a vector as an arrow. The arrow is drawn to point in the direction of the vector quantity, and the length of the arrow is proportional to the magnitude of the vector quantity.

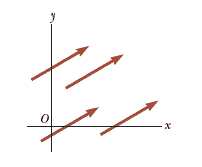Two vectors may be defined to be equal if they have the same magnitude and if they point in the same direction. For example, all the vectors in the figure are equal even though they have different starting points:

This property allows us to move a vector to a position parallel to itself in a diagram without affecting the vector.

Vector addition

The rules for vector addition are conveniently described by a graphical method.

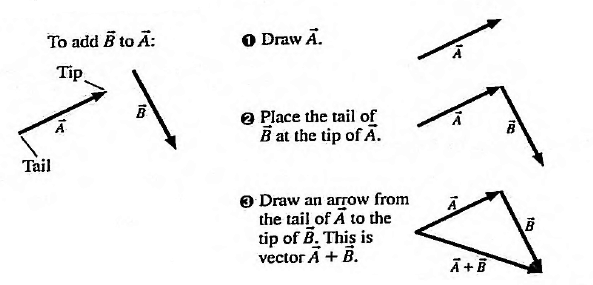To add vector $\vec{B}$ to vector $\vec{A}$, first draw vector $\vec{A}$ on graph paper, with its magnitude represented by a convenient length scale, and then draw vector $\vec{B}$ to the same scale, with its tail starting from the tip of $\vec{A}$. The resultant vector $\vec{R}=\vec{A}+\vec{B}$ is the vector drawn from the tail of $\vec{A}$ to the tip of $\vec{B}$, as shown in the figure:

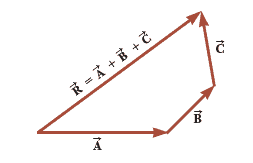A geometric construction can also be used to add more than two vectors, the figure is for the case of three vectors:

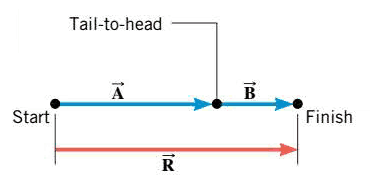The simplest situation occurs when the vectors point along the same direction- that is, when they are colinear:

Here, With the tail of the second arrow located at the head of the first arrow, the two vectors simply add to give the length of the total vector. This kind of vector addition is identical to the familiar addition of two scalar numbers (2 + 3 = 5) and can be carried out here only because the vectors point along the same direction.

Vector subtraction

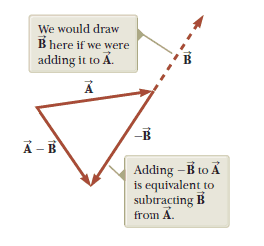The operation of vector subtraction makes use of the definition of the negative of a vector. The vectors $\vec{A}$ and $-\vec{A}$ have the same magnitude but point in opposite directions.

We define the operation $\vec{A} - \vec{B}$ as vector $- \vec{B}$ added to vector $\vec{A}$:

$$\vec{A} - \vec{B}= \vec{A} + (- \vec{B})$$

Scalar multiplication of vectors

If vector $\vec{A}$ is multiplied by a positive scalar quantity $m$, the product $m\vec{A}$ is a vector that has the same direction as $\vec{A}$ and magnitude $mA$.

If vector $\vec{A}$ is multiplied by a negative scalar quantity $-m$, the product $-m\vec{A}$ is directed opposite $\vec{A}$.

Vector product

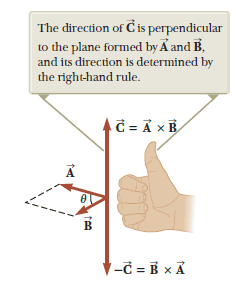Given any two vectors $\vec{A}$ and $\vec{B}$, the vector product $\vec{A} \times \vec{B}$ is defined as a third vector $\vec{C}$, which has a magnitude of $AB \sin \theta$, where $\theta$ is the angle between $\vec{A}$ and $\vec{B}$.

That is, if $\vec{C}$ is given by $\vec{C}= \vec{A} \times \vec{B}$ its magnitude is $C=AB \sin \theta$.

The quantity $AB \sin \theta$ is equal to the area of the parallelogram formed by $\vec{A}$ and $\vec{B}$. The direction of $\vec{C}$ is perpendicular to the plane formed by $\vec{A}$ and $\vec{B}$, and the best way to determine this direction is to use the right hand rule. The four fingers of the right hand are pointed along $\vec{A}$ and then “wrapped” in the direction that would rotate $\vec{A}$ into $\vec{B}$ through the angle $\theta$. The direction of the upright thumb is the direction of $ \vec{A} \times \vec{B}= \vec{C}$.

The Scalar Product of Two Vectors

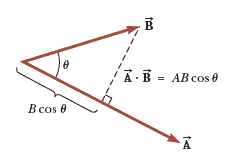The Scalar Product is a way of combining vectors that proves useful in physics. We write the scalar product of any two vectors $\vec{A}$ and $\vec{B}$ as $\vec{A} \cdot \vec{B}$, This scalar product is defined as a scalar quantity equal to the product of the magnitudes of the two vectors and the cosine of the angle $\theta$ between them:

$$\vec{A} \cdot \vec{B}= AB \cos \theta$$

As you can see, $B \cos \theta$ is the projection of $\vec{B}$ onto $\vec{A}$. Therefore, $\vec{A} \cdot \vec{B}$ is the product of the magnitude of $\vec{A}$ and the projection of $\vec{B}$ onto $\vec{A}$.

The graphical method of adding vectors is not recommended whenever high accuracy is required or in three-dimensional problems. In this section, we describe a method of adding vectors that makes use of the projections of vectors along coordinate axes. These projections are called the components of the vector or its rectangular components. Any vector can be completely described by its components.

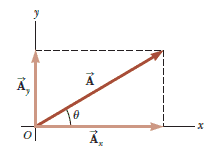
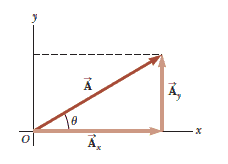Consider a vector $\vec{A}$ lying in the $xy$ plane and making an arbitrary angle $\theta$ with the positive $x$ axis, This vector can be expressed as the sum of two other component vectors $\vec{A_x}$, which is parallel to the $x$ axis, and $\vec{A_y}$, which is parallel to the $y$ axis. From the figure, we see that the three vectors form a right triangle and that $\vec{A} = \vec{A_x} + \vec{A_x}$:

We shall often refer to the “components of a vector $\vec{A}$”, written $A_x$ and $A_y$ (without the vectors notation).

And in the figure, the component vector $\vec{A_y}$ moved to the left so that it lies along the $y$ axis:

We see that the component $A_x$ represents the projection of $\vec{A}$ along the $x$ axis, and the component $A_y$ represents the projection of $\vec{A}$ along the $y$ axis. These components can be positive or negative. The component $A_x$ is positive if the component vector $\vec{A_y}$ points in the positive $x$ direction and is negative if $\vec{A_x}$ points in the negative $x$ direction. A similar statement is made for the component $A_y$.

Hence, the components of $\vec{A}$ are:

$$A_x = A \cos \theta \;\;\;\;\;\;\;\;\;\;\; A_y = A \sin \theta$$

Therefore, the magnitude and direction of $\vec{A}$ are related to its components through the expressions:

$$A = \sqrt{ A_x^2 + A_y^2 } \;\;\;\;\;\;\;\;\; \theta =\tan^{-1} \left( \dfrac{A_y}{A_x} \right)$$

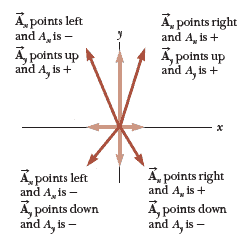Notice that the signs of the components $A_x$ and $A_y$ depend on the angle $\theta$.

When solving problems in two dimensions, you can specify a vector $\vec{A}$ either with its components $A_x$ and $A_y$ or with its magnitude and direction $A$ and $\theta$.

Vector quantities often are expressed in terms of unit vectors. A unit vector is a dimensionless vector having a magnitude of exactly 1.

Unit vectors are used to specify a given direction and have no other physical significance. They are used solely as a bookkeeping convenience in describing a direction in space.

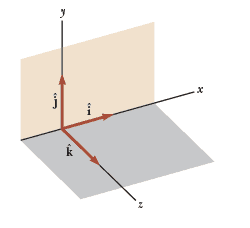
The “hats,” or circumflexes, on the symbols are a standard notation for unit vectors. We shall use the symbols $\hat{i}$, $\hat{j}$ and $\hat{k}$ to represent unit vectors pointing in the positive $x$, $y$, and $z$ directions, respectively.

The magnitude of each unit vector equals 1; that is, $\left| \hat{i} \right| = \left| \hat{j} \right| = \left| \hat{k} \right| =1$.

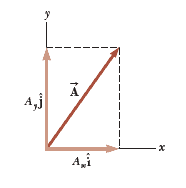Consider a vector $\vec{A}$ lying in the $xy$ plane as shown. The product of the component $A_x$ and the unit vector $\hat{i}$ is the component vector $\vec{A_x}= A_x \hat{i}$, which lies on the $x$ axis and has magnitude $\left| A_x \right|$. Likewise, $\vec{A_y}= A_y \hat{j}$ is the component vector of magnitude $\left| A_y \right|$ lying on the $y$ axis. Therefore, the unit-vector notation for the vector $\vec{A}$ is:

$\vec{A} = A_x \hat{i} + A_y \hat{j}$

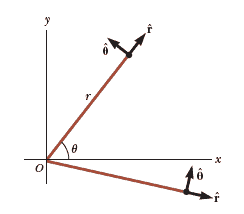Unit vectors for a point described by polar coordinates are radial and angular unit vectors $\hat{r}$ and $\hat{\theta}$. These vectors are also of unit length, however, the directions of radial and angular unit vectors depend on the point, as shown by the point in the fourth quadrant in the figure.

Vector addition

Now let us see how to use components to add vectors when the graphical method is not sufficiently accurate. Suppose we wish to add vector $\vec{B}$ to vector $\vec{A}$, where vector $\vec{B}$ has components $B_x$ and $B_y$. The resultant vector $\vec{R}$ is:

$\vec{R}=\vec{A} + \vec{B}= (A_x \hat{i} + A_y \hat{j}) + (B_x \hat{i} + B_y \hat{j})= (A_x + B_x) \hat{i} + (A_y + B_y) \hat{j}$

Because $\vec{R}= R_x \hat{i} + R_y \hat{j}$, we see that the components of the resultant vector are:

$$R_x =A_x + B_x \;\;\;\;\;\;\;\;\;\; R_y =A_y + B_y$$

Therefore, we see that in the component method of adding vectors, we add all the $x$ components together to find the $x$ component of the resultant vector and use the same process for the $y$ components.

The magnitude of $\vec{R}$ and the angle it makes with the x axis are obtained from its components using the relationships:

$$R = \sqrt{ R_x^2 + R_y^2 }= \sqrt{ (A_x + B_x)^2 + (A_y + B_y)^2 } \;\;\;\;\;\;\;\;\; \theta =\tan^{-1} \left( \dfrac{R_y}{R_x} \right)=\tan^{-1} \left( \dfrac{A_y + B_y}{A_x + B_x} \right)$$

The extension of our methods to three-dimensional vectors is straightforward. If $\vec{A}$ and $\vec{B}$ both have $x$, $y$, and $z$ components, The sum of $\vec{A}$ and $\vec{A}$ is:

$\vec{R}= (A_x + B_x) \hat{i} + (A_y + B_y) \hat{j} + (A_z + B_z) \hat{k}$

If a vector $\vec{R}$ has $x$, $y$, and $z$ components, the magnitude of the vector is:

$$R = \sqrt{ R_x^2 + R_y^2 + R_z^2}$$

The angle $\theta_x$ that $\vec{R}$ makes with the $x$ axis is found from the expression:

$$\theta_x =\cos^{-1} \left( \dfrac{R_x}{R} \right)$$

with similar expressions for the angles with respect to the $y$ and $z$ axes.

Vector product

From the definition of unit vectors, the cross products of the unit vectors obey the following rules:

$$\hat{i} \times \hat{i} = \hat{j} \times \hat{j} = \hat{k} \times \hat{k} = 0$$

$$\hat{i} \times \hat{j} = -\hat{j} \times \hat{i} = \hat{k}$$

$$\hat{j} \times \hat{k} = -\hat{k} \times \hat{j} = \hat{i}$$

$$\hat{k} \times \hat{i} = -\hat{i} \times \hat{k} = \hat{j}$$

The cross product of any two vectors $\vec{A}$ and $\vec{B}$ can be expressed in unit-vector notation by using the following determinant form:

Expanding these determinants gives the result: $$\vec{A} \times \vec{B}= (A_y B_z - A_z B_y) \hat{i} + (A_z B_x - A_x B_z) \hat{j} + (A_x B_y - A_y B_x) \hat{k} $$

The Scalar Product of Two Vectors

The scalar products of the unit vectors are:

$$\hat{i} \cdot \hat{i} = \hat{j} \cdot \hat{j} = \hat{k} \cdot \hat{k} = 1$$

$$\hat{i} \cdot \hat{j} = \hat{i} \cdot \hat{k} = \hat{j} \cdot \hat{k} = 0$$

Using these expressions shows that the scalar product of $\vec{A}$ and $\vec{B}$ reduces to:

$$\vec{A} \cdot \vec{B}= A_x B_x + A_y B_y + A_z B_z$$

In the special case in which $\vec{A} = \vec{B}$, we see that:

$$\vec{A} \cdot \vec{A}= A_x^2 + A_y^2 + A_z^2= A^2$$