Two-dimensional motion could be understood by analyzing the horizontal and vertical components of the motion separately. In other words, the x and y motions are independent of each other. The independence of the x and y motions lies at the heart of two-dimensional motion. It allows us to treat two-dimensional motion as two distinct one-dimensional motions, one for the x direction and one for the y direction. Everything that we have learned about motion in one dimension will now be applied separately to each of the two directions.

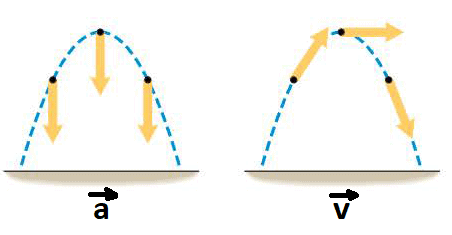
For convenience, we assume that the motion begins at the origin (so $x_i=y_i =0$) at time $t_i =0$, we will treat the horizontal and vertical components of instantaneous velocity $\vec{v}$ and instantaneous acceleration $\vec{a}$ separately, and use positive and negative signs to indicate the direction rather than use full vector notation of motion .In so doing, we will be able to describe the five motion variables of $x$ $(x,v_{x,f}, v_{x,i},a_x,t)$ and $y$ $(y,v_{y,f}, v_{y,i},a_y,t)$ separately and then brimg these descriptions together to understand the two-dimensional picture.

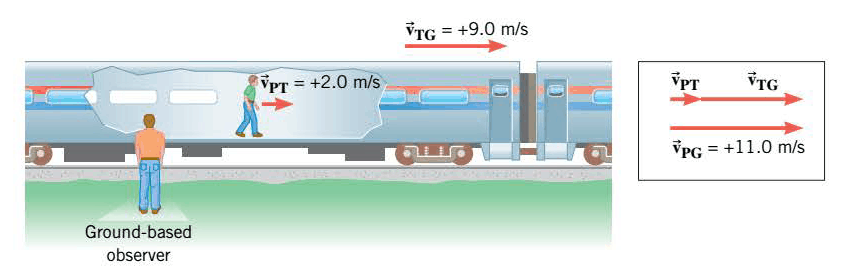
We now consider how observations made in different frames of reference are related to each other. For example, the following figure showing a passenger walking toward the front of a moving train.

The people sitting on the train see the passenger walking with a velocity of +2.0 m/s, where the plus sign denotes a direction to the right. Suppose the train is moving with a velocity of +9.0 m/s relative to an observer standing on the ground. Then the ground-based observer would see the passenger moving with a velocity of + 11 m/s, due in part to the walking motion and in part to the train's motion. As an aid in describing relative velocity, let us define the following symbols:

$\vec{v_{PT}}$ = velocity of the Passenger relative to the Train = +2.0 m/s

$\vec{v_{TG}}$ = velocity of the Train relative to the Ground = +9.0 m/s

$\vec{v_{PG}}$ = velocity of the Passenger relative to the Ground = + 11 m/s

In terms of these symbols, the above situation can be summarized as follows:

$\vec{v_{PG}}= \vec{v_{PT}} + \vec{v_{TG}}$ = 2.0 m/s + 9.0 m/s = + 11.0 m/s

According to the above Equation, $\vec{v_{PG}}$ is the vector sum of $\vec{v_{PT}}$ and $\vec{v_{TG}}$, and this sum is shown in the drawing. When the velocities are along the same line, simple addition or subtraction is sufficient to obtain the relative velocity. But if they are not along the same line, we must make use of vector addition. We emphasize that when specifying a velocity, it is important to specify what the reference frame is. When determining relative velocity, it is easy to make a mistake by adding or subtracting the wrong velocities. It is important, therefore, to draw a diagram and use a careful labeling process. Each velocity is labeled by two subscripts: the first refers to the object, the second to the reference frame in which it has this velocity.

The ordering of the subscript symbols in relative velocity Equation follows a definite pattern. The first subscript (P) on the left side of the equation is also the first subscript on the right side of the equation. Likewise, the last subscript (G) on the left side is also the last subscript on the right side. The third subscript (T) appears only on the right side of the equation as the two "inner" subscripts (the two T’s).

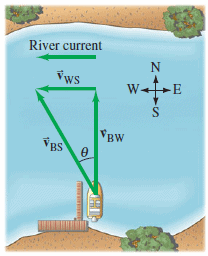
The above rules is also valid for two-dimensional motion. the following figure depicts a common situation that deals with relative velocity in two dimensions, a boat heads directly across a river:

Part a of the drawing shows a boat being carried downstream by a river; the engine of the boat is turned off. In part b, the engine is turned on, and now the boat moves across the river in a diagonal fashion because of the combined motion produced by the current and the engine. The list below gives the velocities for this type of motion and the objects relative to which they are measured:

$\vec{v_{BS}}$ = velocity of the Boat relative to the Shore.

$\vec{v_{BW}}$ = velocity of the Boat relative to the Water (what the boat’s motor produces).

$\vec{v_{WS}}$ = velocity of the Water relative to the Shore (river current).

Therefore, the velocity of the boat relative to the shore is:

$\vec{v_{BS}}= \vec{v_{BW}} + \vec{v_{WS}}$

This equation is valid in general and can be extended to three or more velocities. For example, if a fisherman on the boat walks with a velocity $\vec{v_{FB}}$ relative to the boat, his velocity relative to the shore is $\vec{v_{FS}}= \vec{v_{FB}} + \vec{v_{BW}} + \vec{v_{WS}}$ The equations involving relative velocity will be correct when adjacent inner subscripts are identical and when the outermost ones correspond exactly to the two on the velocity on the left of the equation. But this works only with plus signs (on the right), not minus signs.

It is often useful to remember that for any two objects or reference frames, A and B, the velocity of A relative to B has the same magnitude, but opposite direction, as the velocity of B relative to A:

$$\vec{v_{BA}}= -\vec{v_{AB}}$$

For example, if a train is traveling 100 km/h relative to the Earth in a certain direction, objects on the Earth (such as trees) appear to an observer on the train to be traveling 100 km/h in the opposite direction.

Let us now consider two-dimensional motion during which the acceleration of a particle remains constant in both magnitude and direction. As we shall see, this approach is useful for analyzing some common types of motion.

Displacement

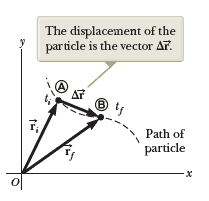
In two dimensions, we indicate its position by its position vector $\vec{r}$ , drawn from the origin of some coordinate system to the location of the particle in the xy plane as in the following Figure, the particle is at point A, described by position vector $\vec{r_i}$. At some later time it is at point B, described by position vector $\vec{r_f}$. The path followed by the particle from A to B is not necessarily a straight line:

As we learned in one-dimensional motions, displacement is a vector, and the displacement of the particle is the difference between its final position and its initial position. We now define the displacement vector for a particle such as the one in the above Figure as the difference between its final position vector and its initial position vector and the direction of displacement vector is indicated in the Figure. As we see from the figure, the magnitude of displacement vector is less than the distance traveled along the curved path followed by the particle.

Velocity

We define the average velocity $\bar{\vec{v}}$ of a particle during the time interval $\Delta t$ as the displacement of the particle divided by the time interval. Multiplying or dividing a vector quantity by a positive scalar quantity such as $\Delta t$ changes only the magnitude of the vector, not its direction. Because displacement is a vector quantity and the time interval is a positive scalar quantity, we conclude that the average velocity is a vector quantity directed along displacement vector.

The average velocity between points is independent of the path taken. That is because average velocity is proportional to displacement, which depends only on the initial and final position vectors and not on the path taken. As with onedimensional motion, we conclude that if a particle starts its motion at some point and returns to this point via any path, its average velocity is zero for this trip because its displacement is zero.

 

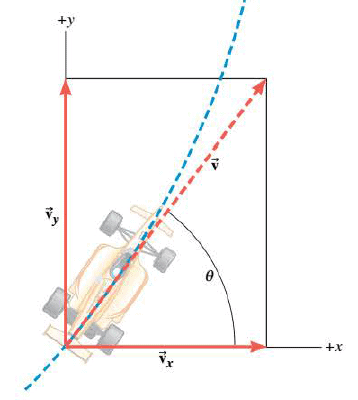
The instantaneous velocity $\vec{v}$ is defined as the limit of the average velocity as $\Delta t$ approaches zero, so the velocity vector at each instant is always tangent to the path.

The following figure illustrates that the instantaneous velocity $\vec{v}$ is tangent to the path of the car. The drawing also shows the vector components $\vec{v_x}$ and $\vec{v_y}$ of the velocity, which are parallel to the x and y axes, respectively.

Acceleration

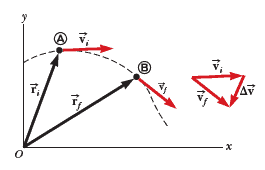
As a particle moves from one point to another along some path, its instantaneous velocity vector changes. Knowing the velocity at these points allows us to determine the average acceleration of the particle. The average acceleration $\bar{\vec{a}}$ of a particle is defined as the change in its instantaneous velocity vector $\vec{\Delta v}$ divided by the time interval $\Delta t$ during which that change occurs:

Because average acceleration is the ratio of a vector quantity $\vec{\Delta v}$ and a positive scalar quantity $\Delta t$, we conclude that average acceleration is a vector quantity directed along $\vec{\Delta v}$ .

 

The average acceleration $\bar{\vec{a}}$ becomes equal to the instantaneous acceleration $\vec{a}$ if the change in velocity is constant or the motion is with constant acceleration.

Because the acceleration of the particle is assumed constant in this discussion, its components $a_x$ and $a_y$ also are constants. Therefore, we can model the particle as a particle under constant acceleration independently in each of the two directions and apply the equations of kinematics separately to the x and y components of the velocity vector.

 

To understand how displacement, velocity, and acceleration are applied to two-dimensional motion, consider a spacecraft equipped with two engines that are mounted perpendicular to each other. These engines produce the only forces that the craft experiences, and the spacecraft is assumed to be at the coordinate origin when $t_i=0 \;s$:

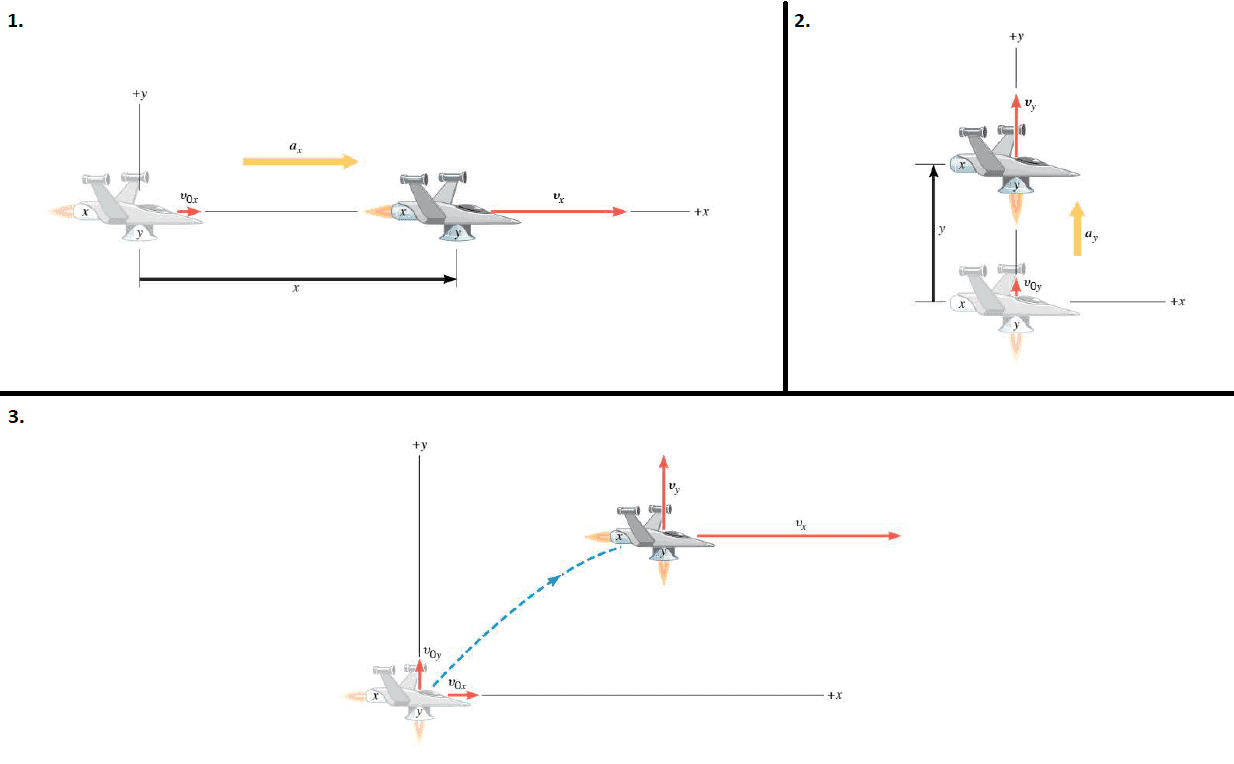
• 1. only the engine oriented along the x direction is firing, and the vehicle accelerates along this direction. It is assumed that the velocity in the y direction is zero, and it remains zero, since the y engine is turned off. The motion of the spacecraft along the x direction is described by the five kinematic variables $x, a_x, v_xf, v_xi,$ and t. If the spacecraft has a constant acceleration along the x direction, the equations of kinematics can be used. For convenience, these equations are written in the left column of the following table.
• 2. now only the y engine is firing, and the spacecraft accelerates along the y direction. Such a motion can be described in terms of the kinematic variables $y, a_y, v_yf, v_yi,$ and t. And if the acceleration along the y direction is constant, these variables are related by the equations of kinematics, as written in the right column of the following table.
• 3. both engines of the spacecraft are firing at the same time, the resulting motion takes place in part along the x axis and in part along the y axis, as the Figure illustrates. The thrust of each engine gives the vehicle a corresponding acceleration component. The x engine accelerates the craft in the x direction and causes a change in the x component of the velocity. Likewise, the y engine causes a change in the y component of the velocity.

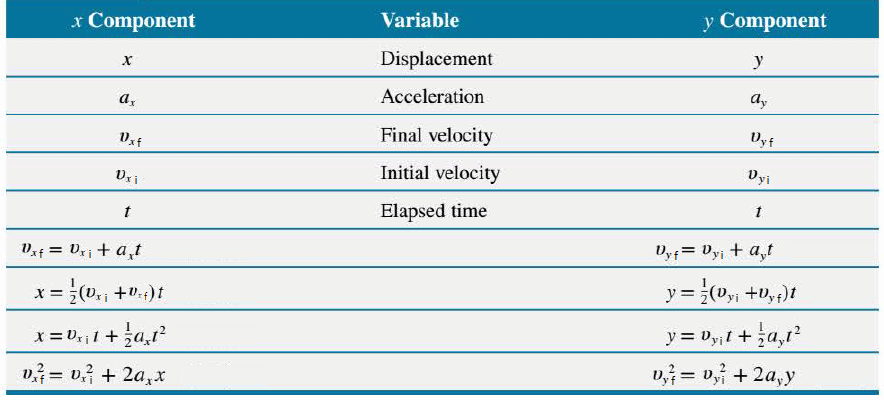
So, the horizontal and vertical components of a two-dimensional motion are completely independent of each other and can be handled separately, with time t as the common variable for both components.

Here we examine the more general translational motion of objects moving through the air in two dimensions near the Earth’s surface, such as a golf ball, a thrown or batted baseball, kicked footballs, and speeding bullets. These are all examples of projectile motion.

Although air resistance is often important, in many cases its effect can be ignored, and we will ignore it in the following analysis. We will not be concerned now with the process by which the object is thrown or projected. We consider only its motion after it has been projected, and before it lands or is caught—that is, we analyze our projected object only when it is moving freely through the air under the action of gravity alone. Then the acceleration of the object is that due to gravity, which acts downward with magnitude $g= 9.8 \;\mathrm{m/s^2}$, and we assume it is constant.

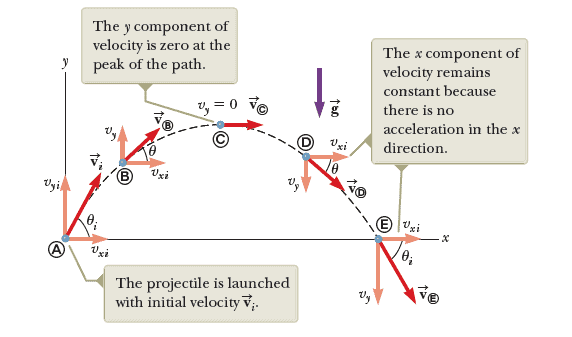
We consider the horizontal and vertical parts of the motion separately. In the horizontal or x direction, the moving object (the projectile) does not slow down in the absence of air resistance. Thus, the x component of the velocity remains constant at its initial value or $v_{xi} = v_{xf}$, and the x component of the acceleration is $a_x= 0 \;\mathrm{m/s^2}$. In the vertical or y direction, however, the projectile experiences the effect of gravity. As a result, the y component of the velocity is not constant and changes. The y component of the acceleration $a_y$ is the downward acceleration due to gravity. If the path or trajectory of the projectile is near the earth's surface, $a_y$ has a magnitude of $9.80 \;\mathrm{m/s^2}$. Then, the phrase "projectile motion" means that $a_x= 0 \;\mathrm{m/s^2}$ ($v_{xi} = v_{xf}=v_x$) and $a_y$ equals the acceleration due to gravity $g$.

Trajectories Depend upon the Viewer

Suppose you toss a ball up and catch it while riding in a bus. To you, the ball would seem to go straight up and straight down. But what would an observer on the sidewalk see? The observer would see the ball leave your hand, rise up, and return to your hand, but because the bus would be moving, your hand also would be moving. The bus, your hand, and the ball would all have the same horizontal velocity. Thus, the trajectory of the ball would be similar to that of Projectiles Launched at an Angle.

To show that the path followed by any projectile is a parabola, we need to find y as a function of x by eliminating between the two equations for horizontal and vertical motion:

$$x=v_x t$$ $$y = v_{yi}t + \frac{1}{2} a_y t^2 = v_{yi}t - \left(\frac{1}{2} g t^2 \right)$$

From the first equation, we have $\left(t=\dfrac{x}{v_x}\right)$ and we substitute this into the second one to obtain:

$$y = \left(\dfrac{v_{yi}}{v_x} \right) x - \left( \dfrac{g}{2 v_x^2} \right) x^2$$

We see that y as a function of x has the form $y = A x - B x^2$ where A and B are constants for any specific projectile motion. This is the standard equation for a parabola.

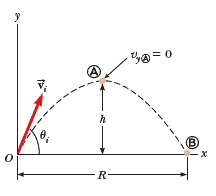
Assume a projectile is launched from the origin at $t_i = 0 \;s$ and returns to the same horizontal level as shown in Figure:

This situation is common in sports, where baseballs, footballs, and golf balls often land at the same level from which they were launched.

Two points in this motion are especially interesting to analyze: the peak point A, which has Cartesian coordinates (R/2, h), and the point B, which has coordinates (R, 0). The distance R is called the horizontal range of the projectile, and the distance h is its maximum height. Let us find h and R mathematically in terms of $v_i$, $\theta_i$, and $g$.

We can determine h by noting that at the peak $v_y= 0$. Therefore, from the particle under constant acceleration model, we can determine the time $t_A$ at which the projectile reaches the peak:

$$v_{yf}= v_{yi} + a_y t$$ $$0= v_i \sin \theta_i - gt_A$$ $$ t_A=\dfrac{v_i \sin \theta_i}{g}$$

 

$$y = v_{yi}t + \frac{1}{2} a_y t^2$$ $$h= (v_i \sin \theta_i) \left( \dfrac{v_i \sin \theta_i}{g} \right) - \left(\frac{1}{2} g \left( \dfrac{v_i \sin \theta_i}{g} \right)^2 \right)$$ $$ h= \dfrac{v_i^2 \sin^2 \theta_i}{2g}$$

Because of the symmetry of the trajectory, the projectile covers the upward part of the trajectory to the top in exactly the same time interval as it requires to come back to the ground from the topmost point $t_B = 2t_A$.

Therefore, the range R is the horizontal position of the projectile at a time that is twice the time at which it reaches its peak. Using the particle under constant velocity model:

$$ x_B = v_x t_B$$ $$R= (v_i \cos \theta_i) (2t_A) = (v_i \cos \theta_i) \left( \dfrac{v_i \sin \theta_i}{g} \right)= \dfrac{v_i^2 (2 \sin \theta_i \cos \theta_i)}{g}$$ $$R= \dfrac{v_i^2 \sin 2\theta_i }{g}$$

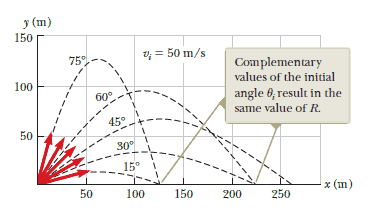
From the above equation we see that the maximum value of R is $R_{max}= \dfrac{v_i^2}{g}$, this happend when $\sin 2\theta_i = 1$ (maximum value), which occurs when $2\theta_i = 90^o$. Therefore, R is a maximum when $\theta_i = 45^o$.

So far, air resistance has been ignored in the analysis of projectile motion. While the effects of air resistance are very small for some projectiles, for others, the effects are large and complex. For example, dimples on a golf ball reduce air resistance and maximize its range. In baseball, the spin of the ball creates forces that can deflect the ball. For now, just remember that the force due to air resistance does exist and it can be important.