We discussed early experiments that combined classical concepts with new quantum concepts. Once physicists were convinced that quantum behavior was real, a brand-new avenue was opened up for theoretical research, leading to the development of quantum mechanics. This an extremely successful theory for explaining the behavior of microscopic particles. Here, we will see how the theory can be built from our new quantum concepts in combination with material on waves and the waves under boundary conditions model. Once we have established this theory, it will become the basis for our understanding of atoms, molecules, nuclei, and elementary particles.

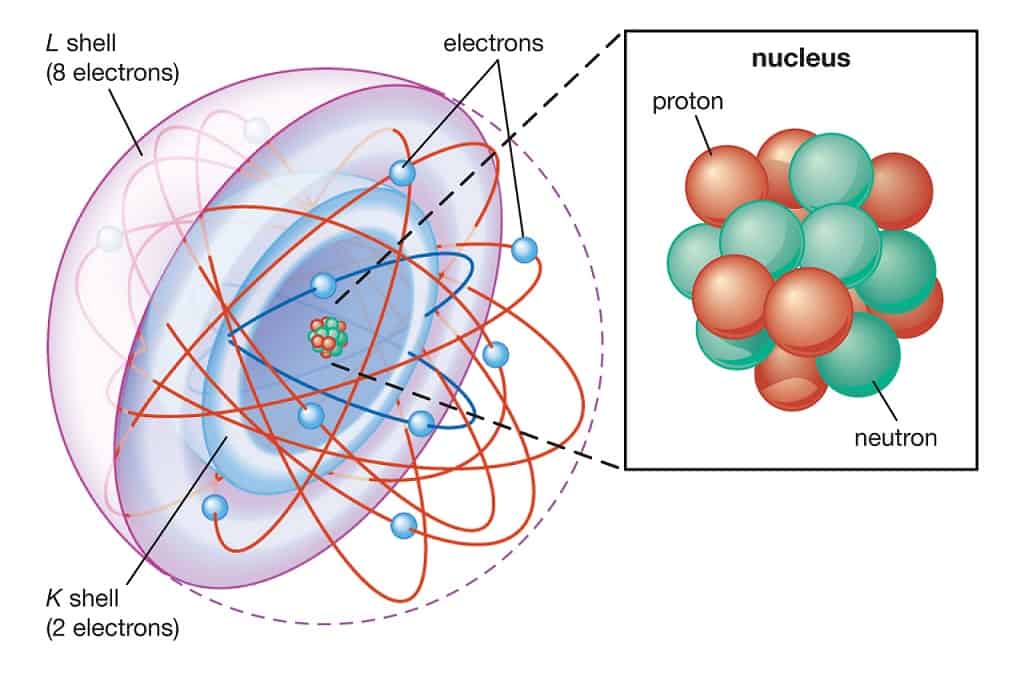
An atom contains a small, positively charged nucleus (radius $\approx 10^{-15}$ m), which is surrounded at relatively large distances (radius $\approx 10^{-10}$ m) by a number of electrons. In the natural state, an atom is electrically neutral because the nucleus contains a number of protons (each with a charge of +e) that equals the number of electrons (each with a charge of -e). This model of the atom is universally accepted now and is referred to as the nuclear atom.

The nuclear atom is a relatively recent idea. In the early part of the twentieth century a widely accepted model, developed by the English physicist Joseph J. Thomson (1856-1940), pictured the atom very differently. In Thomson's view there was no nucleus at the center of an atom. Instead, the positive charge was assumed to be spread throughout the atom, forming a kind of paste or pudding, in which the negative electrons were suspended like plums.

The "plum-pudding" model was discredited in 1911 when the New Zealand physicist Ernest Rutherford (1871-1937) published experimental results that the model could not explain. Rutherford and his coworkers directed a beam of alpha particles ($\alpha$ particles) at a thin metal foil made of gold. Alpha particles are positively charged particles (the nuclei of helium atoms, although this was not recognized at the time) emitted by some radioactive materials.

But how could the electrons in a nuclear atom remain separated from the positively charged nucleus? If the electrons were stationary, they would be pulled inward by the attractive electric force of the nuclear charge. Therefore, the electrons must be moving around the nucleus in some fashion, like planets in orbit around the sun. In fact, the nuclear model of the atom is sometimes referred to as the "planetary" model. The dimensions of the atom, however, are such that it contains a larger fraction of empty space than our solar system does

Although the planetary model of the atom is easy to visualize, it too is fraught with difficulties. For instance, an electron moving on a curved path has a centripetal acceleration, as Uniform Circular Motion discusses. And when an electron is accelerating, it radiates electromagnetic waves, as Electromagnetic Waves discusses. These waves carry away energy. With their energy constantly being depleted, the electrons would spiral inward and eventually collapse into the nucleus. Since matter is stable, such a collapse does not occur. Thus, the planetary model, although providing a more realistic picture of the atom than the "plum-pudding" model, must be telling only part of the story. The full story of atomic structure is fascinating, and here we describes another aspect of it.

Line Spectra

We have seen that all objects emit electromagnetic waves. For a solid object, such as the hot filament of a light bulb, these waves have a continuous range of wavelengths, some of which are in the visible region of the spectrum. The continuous range of wavelengths is characteristic of the entire collection of atoms that make up the solid. In contrast, individual atoms, free of the strong interactions that are present in a solid, emit only certain specific wavelengths rather than a continuous range. These wavelengths are characteristic of the atom and provide important clues about its structure. To study the behavior of individual atoms, low-pressure gases are used in which the atoms are relatively far apart.

The simplest line spectrum is that of atomic hydrogen, and much effort has been devoted to understanding the pattern of wavelengths that it contains. The spectrum of atomic hydrogen schematic form some of the groups or series of lines. Only one of the groups is in the visible region of the electromagnetic spectrum; it is known as the Balmer series, in recognition of Johann J. Balmer (1825-1898), a Swiss schoolteacher who found an empirical equation that gave the values for the observed wavelengths. This equation along with similar equations that apply to the Lyman series at shorter wavelengths and the Paschen series at longer wavelengths are useful because they reproduce the wavelengths that hydrogen atoms radiate. However, these equations are empirical and provide no insight as to why certain wave-lengths are radiated and others are not.

It was the great Danish physicist, Niels Bohr ( 1885-1962), who provided the first model of the atom that predicted the discrete wavelengths emitted by atomic hydrogen. Bohr's model started us on the way toward understanding how the structure of the atom restricts the radiated wavelengths to certain values. In 1922 Bohr received the Nobel Prize in physics for his accomplishment.

The Bohr Model

In 1913 Bohr presented a model that led to equations such as Bahner's for the wavelengths that the hydrogen atom radiates. Bohr's theory begins with Rutherford's picture of an atom as a nucleus surrounded by electrons moving in circular orbits. In his theory, Bohr made a number of assumptions and combined the new quantum ideas of Planck and Einstein with the traditional description of a particle in uniform circular motion.

The Energies and Radii of the Bohr Orbits

Radii for Bohr orbits (in meters):

$$ r_n = (5.29 \times 10^{-11}) \dfrac{n^2}{Z} \;\;\;\;\;\;\;\; n= 1, 2, 3, ... $$

Bohr energy levels in joules:

$$ E_n = -(2.18 \times 10^{-18}) \dfrac{Z^2}{n^2} \;\;\;\;\;\;\;\; n= 1, 2, 3, ... $$

Bohr energy levels in electron volts:

$$ E_n = -(13.8) \dfrac{Z^2}{n^2} \;\;\;\;\;\;\;\; n= 1, 2, 3, ... $$

The Line Spectra of the Hydrogen Atom

To predict the wavelengths in the line spectrum of the hydrogen atom, Bohr combined his ideas about atoms ( electron orbits are stationary orbits and the angular momentum of an electron is quantized) with Einstein's idea of the photon.

De Broglie's Explanation of Bohr's Assumption About Angular Momentum

Of all the assumptions Bohr made in his model of the hydrogen atom, perhaps the most puzzling is the assumption about the angular momentum of the electron [$L_n = mv_nr_n = nh/(2\pi)$; n = 1, 2, 3, ... ]. Why should the angular momentum have only those values that are integer multiples of Planck's constant divided by $2 \pi$? In 1923, ten years after Bohr's work, de Broglie pointed out that his own theory for the wavelength of a moving particle could provide an answer to this question.

In de Broglie's way of thinking, the electron in its circular Bohr orbit must be pictured as a particle wave. And like waves traveling on a string, particle waves can lead to standing waves under resonant conditions.

The picture of the hydrogen atom that quantum mechanics and the Schrodinger equation provide differs in a number of ways from the Bohr model. The Bohr model uses a single integer number n to identify the various electron orbits and the associated energies. Because this number can have only discrete values, rather than a continuous range of values, n is called a quantum number. In contrast, quantum mechanics reveals that four different quantum numbers are needed to describe each state of the hydrogen atom. These four are described as follows:

1. The principal quantum number n: As in the Bohr model, this number determines the total energy of the atom and can have only integer values: n = 1, 2, 3, .... In fact, the Schrodinger equation predicts (This prediction requires that small relativistic effects and small interactions within the atom be ignored, and assumes that the hydrogen atom is not located in an external magnetic field) that the energy of the hydrogen atom is identical to the energy obtained from the Bohr model: $E_n = -(13.6 eV) Z^2/n^2$.

2. The orbital quantum number $l$: This number determines the angular momentum of the electron due to its orbital motion. The values that $l$ can have depend on the value of n, and only the following integers are allowed: $l$ =0, 1,2, ... , (n-l)

For instance, if n = 1, the orbital quantum number can have only the value $l$ = 0, but if n = 4, the values $l$ = 0, 1, 2, and 3 are possible. The magnitude $L$ of the angular mon1entum of the electron is:

$$ L= \sqrt{l (l+1)} \dfrac{h}{2 \pi}$$

3. The magnetic quantum number $m_l$: The word "magnetic" is used here because an externally applied magnetic field influences the energy of the atom, and this quantum number is used in describing the effect. Since the effect was discovered by the Dutch physicist Pieter Zeeman (1865-1943), it is known as the Zeeman effect. When there is no external magnetic field, $m_l$ plays no role in determining the energy. In either event, the magnetic quantum number determines the component of the angular momentum along a specific direction, which is called the z direction by convention. The values that $m_l$ can have depend on the value of $l$, with only the following positive and negative integers being permitted: $m_l = -l, ... , - 2, - 1, 0, + 1, + 2, . . . , + l$

For example, if the orbital quantum number is $l$ = 2, then the magnetic quantum number can have the values $m_l$ = -2, -1, 0, + 1, and + 2. The component $L_z$ of the angular momentum in the z direction is:

$$ L_z= m_l \dfrac{h}{2 \pi}$$

4. The spin quantum number $m_s$: This number is needed because the electron has an intrinsic property called "spin angular momentum." Loosely speaking, we can view the electron as spinning while it orbits the nucleus, analogous to the way the earth spins as it orbits the sun. There are two possible values for the spin quantum number of the electron: $m_l= +\frac{1}{2}$ or $m_l= -\frac{1}{2}$

Sometimes the phrases "spin up" and "spin down" are used to refer to the directions of the spin angular momentum associated with the values for $m_s$

 

One set of values for n, $l$, $m_l$, and $m_s$ corresponds to one state. As the principal quantum number n increases, the number of possible combinations of the four quantum numbers rises rapidly.

Quantum mechanics provides a more accurate picture of atomic structure than does the Bohr model. It is important to realize that the two pictures differ substantially.

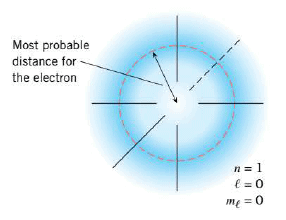According to the Bohr model, the nth orbit is a circle of radius $r_n$, and every time the position of the electron in this orbit is measured, the electron is found exactly at a distance $r_n$ away from the nucleus. This simplistic picture is now known to be incorrect, and the quantum mechanical picture of the atom has replaced it. Suppose that the electron is in a quantum mechanical state for which n = l, and we imagine making a number of measurements of the electron's position with respect to the nucleus. We would find that its position is uncertain, in the sense that there is a probability of finding the electron sometimes very near the nucleus, sometimes very far from the nucleus, and sometimes at intermediate locations. The probability is determined by the wave function $\psi$, as we discusses before. We can make a three-dimensional picture of our findings by marking a dot at each location where the electron is found. More dots occur at places where the probability of finding the electron is higher, and after a sufficient number of measurements, a picture of the quantum mechanical state emerges. The Figure shows the spatial distribution for the position of an electron in a state for which n = 1, $l$ = 0, and $m_l$ = 0. This picture is constructed from so many measurements that the individual dots are no longer visible but have merged to form a kind of probability "cloud" whose density changes gradually from place to place. The dense regions indicate places where the probabiility of finding the electron is higher, and the less dense regions indicate places where the probability is lower. Also indicated in the Figure is the radius where quantum mechanics predicts the greatest probability per unit radial distance of finding the electron in the n = l state. This radius matches exactly the radius of 55 .29 \times 10^{-11}$ m found for the first Bohr orbit.

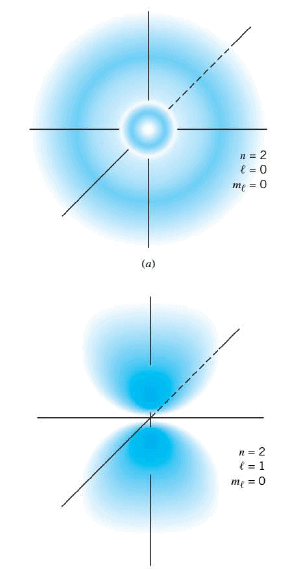For a principal quantum number of n = 2, the probability clouds are different than for n = 1. In fact, more than one cloud shape is possible because with n = 2 the orbital quantum number can be either $l$ = 0 or $l$ = l . Although the value of $l$ does not affect the energy of the hydrogen atom, the value does have a significant effect on the shape of the probability clouds. The first Figure shows the cloud for n = 2, $l$ = 0, and $m_l$ = 0. The second part of the drawing shows that when n = 2, $l$ = 1, and $m_l$ = 0, the cloud has a two-lobe shape with the nucleus at the center between the lobes. For larger values of n, the probability clouds become increasingly complex and are spread out over larger volumes of space.

The probability cloud picture of the electron in a hydrogen atom is very different from the well-defined orbit of the Bohr model. The fundan1ental reason for this difference is to be found in the Heisenberg uncertainty principle.

The Pauli Exclusion Principle

Except for hydrogen, all electrically neutral atoms contain more than one electron, with the number given by the atomic number Z of the element. In addition to being attracted by the nucleus, the electrons repel each other. This repulsion contributes to the total energy of a multiple-electron atom. As a result, the one-electron energy expression for hydrogen, $E_n= -(13.6 eV) Z^2/n^2$, does not apply to other neutral atoms. However, the simplest approach for dealing with a multiple-electron atom still uses the four quantum numbers n, $l$, $m_l$, and $m_s$.

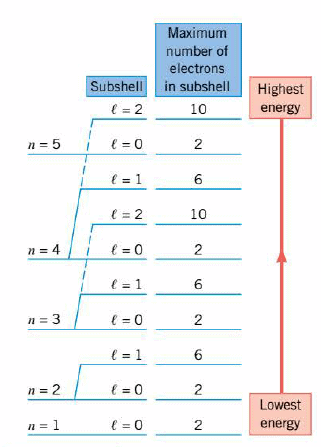
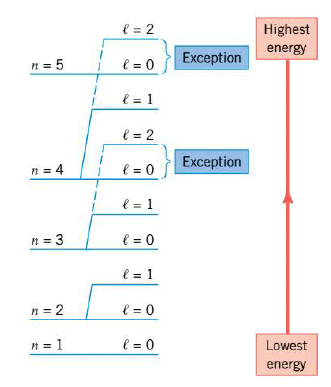Detailed quantum mechanical calculations reveal that the energy level of each state of a multiple-electron atom depends on both the principal quantum number n and the orbital quantum number $l$. The Figure illustrates that the energy generally increases as n increases, but there are exceptions, as the drawing indicates. Furthermore, for a given n, the energy also increases as $l$ increases.

In a multiple-electron atom, all electrons with the same value of n are said to be in the same shell. Electrons with n = 1 are in a single shell (sometimes called the K shell), electrons with n = 2 are in another shell (the L shell), those with n = 3 are in a third shell (the M shell), and so on. Those electrons with the same values for both n and $l$ are often referred to as being in the same subshell. The n= 1 shell consists of a single $l$ = 0 subshell. Then= 2 shell has two subshells, one with $l$ = 0 and one with $l$ = 1. Similarly, then = 3 shell has three subshells, one with $l$ = 0, one with $l$ = 1, and one with $l$ = 2.

In the hydrogen atom near room temperature, the electron spends most of its time in the lowest energy level, or ground state-namely, in the n= l shell. Similarly, when an atom contains more than one electron and is near room temperature, the electrons spend most of their time in the lowest energy levels possible. The lowest energy state for an atom is called the ground state. However, when a multiple-electron atom is in its ground state, not every electron is in then = 1 shell in general because the electrons obey a principle discovered by the Austrian physicist Wolfgang Pauli (1900-1958).

THE PAULI EXCLUSION PRINCIPLE: No two electrons in an atom can have the same set of values for the four quantum numbers n, $l$, $m_l$, and $m_s$.

Suppose two electrons in an atom have three quantum numbers that are identical: n = 3, $m_l$ = l , and $m_s = -\frac{1}{2}$. According to the exclusion principle, it is not possible for each to have $l$ = 2, for example, since each would then have the same four quantum numbers. Each electron must have a different value for $l$ (for instance, $l$ = 1 and $l$ = 2) and, consequently, would be in a different subshell. With the aid of the Pauli exclusion principle, we can determine which energy levels are occupied by the electrons in an atom in its ground state.

Because of the Pauli exclusion principle, there is a maximum number of electrons that can fit into an energy level or subshell. The n= 1, $l$ = 0 subshell can hold at most two electrons. The n = 2, $l$ = l subshell, however, can hold six electrons because with $l$ = l , there are three possibilities for $m_l$ (-1, 0, and + 1), and for each of these choices, the value of $m_s$ can be $+\frac{1}{2}$ or $-\frac{1}{2}$. In general, $m_l$ can have the values 0, $\pm$ 1, $\pm$ 2, . .. , $\pm l$, for 2$l$+1 possibilities. Since each of these can be combined with two possibilities for $m_s$, the total number of different combinations for $m_l$ and $m_s$ is 2(2$l$ + 1). This, then, is the maximum number of electrons the $l$th subshell can hold, as the Figure summarizes.

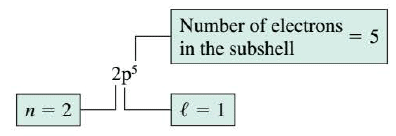For historical reasons, there is a widely used convention in which each subshell of an atom is referred to by a letter rather than by the value of its orbital quantum number $l$. For instance, an $l$ = 0 subshell is called an s subshell. An $l$ = 1 subshell and an $l$ = 2 subshell are known as p and d subshells, respectively. The higher values of $l$= 3, 4, and so on, are referred to as f, g, and so on, in alphabetical sequence.

This convention of letters is used in a shorthand notation that is convenient for indicating simultaneously the principal quantum number n, the orbital quantum number $l$, and the number of electrons in the n,$l$ subshell. An example of this notation is in the Figure.

With this notation, the arrangement, or configuration, of the electrons in an atom can be specified efficiently.

rays. X-rays were discovered by the Dutch physicist Wilhelm K. Roentgen (1845-1923), who performed much of his work in Germany. X-rays can be produced when electrons, accelerated through a large potential difference, collide with a metal target made, for example, from molybdenum or platinum. The target is contained within an evacuated glass tube.

The laser is one of the most useful inventions of the twentieth century. Today, there are many types of lasers, and most of them work in a way that depends directly on the quantum mechanical structure of the atom.