What do you think of when you hear the phrase “theory of relativity”? A white-haired Einstein? $E=mc^2$ ? Black holes? Time travel? There is, without doubt, a certain mystique associated with relativity, an aura of the strange and exotic. The good news is that understanding the ideas of relativity is well within your grasp. Einstein’s special theory of relativity, the portion of relativity we’ll study, is not mathematically difficult at all. The challenge is conceptual because relativity questions deeply held assumptions about the nature of space and time. In fact, that’s what relativity is all about—space and time.

In Newtonian mechanics, space and time are absolute quantities; the length of a meter stick and the time between ticks of a clock are the same to any observer, whether moving or not. But relativity challenges these commonsense notions. As we’ll see, ground-based observers measure the length of a fast-moving rocket to be shorter, and a clock on the rocket to run slower, compared to when the rocket is at rest.

Because relativity challenges our basic notions about space and time, to make progress we will have to exercise the utmost care with regard to logic and precision. We will need to state very precisely just how it is that we know things about the physical world and then ruthlessly follow the logical consequences. The challenge is to stay on this path and not to let our prior assumptions—assumptions that are deeply ingrained in all of us—lead us astray.

 

A bird flies through the air. How fast is it moving? This is a question that doesn’t have a unique answer. The bird might be moving at 10 m/s relative to the air, but only 6 m/s relative to the ground if it is flying into a 4 m/s headwind. To answer the question “How fast is the bird moving?” you need to first answer another question: “Relative to what?” We explored this idea of relative motion back in Projectile Motion Section. This notion of relativity will become even more important here. We’ll find that seemingly straightforward questions don’t have straightforward answers. If you ask, “What time is it?” there is, surprisingly, not a unique answer. Time is, as we’ll see, also relative.

Einstein’s first paper on relativity dealt exclusively with objects that move relative to each other with constant velocity. Motion at constant velocity is a “special case” of motion—namely, motion for which the acceleration is zero. Hence Einstein’s first theory of relativity has come to be known as special relativity. It is “special” in the sense of being a restricted, particular case of a more general theory that came later, not special in the everyday sense meaning distinctive or exceptional.

Events and Inertial Reference Frames

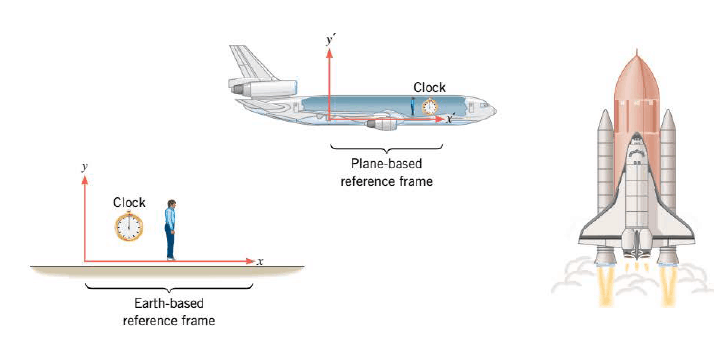
In the theory of special relativity, an event, such as the launching of the space shuttle, is a physical "happening" that occurs at a certain place and time. If two observers are watching the lift-off, one standing on the earth and one in an airplane that is flying at a constant velocity relative to the earth. To record the event, each observer uses a reference frame that consists of a set of x, y, z axes ( called a coordinate system) and a clock. The coordinate systems are used to estalblish where the event occurs, and the clocks to specify when. Each observer is at resit relative to his own reference frame. However, the earth-based observer and the airborne observer are moving relative to each other and so, also, are their respective reference frames.

The theory of special relativity deals with a "special" kind of reference frame, called an inertial reference frame. As Newton's Laws of Motion Section discusses, an inertial reference frame is one in which Newton's law of inertia is valid. That is, if the net force acting on a body is zero, the body either remains at rest or moves at a constant velocity. In other words, the acceleration of such a body is zero when measured in an inertial reference frame. Rotating and otherwise accelerating reference frames are not inertial reference frames. The earth-based reference frame in is not quite an inertial frame because it is subjected to centripetal accelerations as the earth spins on its axis and revolves around the sun. In most situations, however, the effects of these accelerations are small, and we can neglect them. To the extent that the earth-based reference frame is an inertial frame, so is the plane-based reference frame, because the plane moves at a constant velocity relative to the earth.

The Postulates

Einstein built his theory of special relativity on two fundamental assumptions or postulates about the way nature behaves:

1. The Relativity Postulate: The laws of physics are the same in every inertial reference frame.

2. The Speed-of-Light Postulate: The speed of light in a vacuum, measured in any inertial reference frame, always has the same value of c, no matter how fast the source of light and the observer are moving relative to each other.

The remainder of this article reexamines, from the viewpoint of special relativity, a number of fundamental concepts that have been discussed earlier from the viewpoint of classical physics. These concepts are time, length, momentum, kinetic energy, and the addition of velocities. We will see that each is modified by special relativity in a way that depends on the speed v of a moving object relative to the speed c of light in a vacuum.

when the object moves slowly [vis much smaller than c ($v \ll c$)], the modification is negligibly small, and the classical version of each concept provides an accurate description of reality. However, when the object moves so rapidly that v is an appreciable fraction of the speed of light [v is approximately equal to c ($v \approx c$)], the effects of special relativity must be considered. The gold panel in the Figure lists the various equations that convey the modifications imposed by special relativity. Each of these equations will be discussed in later sections.

It is important to realize that the modifications imposed by special relativity do not imply that the classical concepts of time, length, momentum, kinetic energy, and the addition of velocities, as developed by Newton and others, are wrong. They are just limited to speeds that are very small compared to the speed of light. In contrast, the relativistic view of the concepts applies to all speeds between zero and the speed of light.

Common experience indicates that time passes just as quickly for a person standing on the ground as it does for an astronaut in a spacecraft. In contrast, special relativity reveals that the person on the ground measures time passing more slowly for the astronaut than for herself.

Since speed is distance divided by time and the time is different for the two observers, it follows that the distances must also be different, if the relative speed is to be the same for both individuals.

Recall from that when two or more objects interact, the principle of conservation of linear momentum applies if the system of objects is isolated. This principle states that the total linear momentum of an isolated system remains constant at all times. (An isolated system is one in which the sum of the external forces acting on the objects is zero.) The conservation of linear momentum is a law of physics and, in accord with the relativity postulate, is valid in all inertial reference frames. That is, when the total linear momentum is conserved in one inertial reference frame, it is conserved in all inertial reference frames. So The total relativistic momentum of an isolated system is conserved in all inertial reference frames.

One of the most astonishing results of special relativity is that mass and energy are equivalent, in the sense that a gain or loss of mass can be regarded equally well as a gain or loss of energy. Consider, for example, an object of mass m traveling at a speed v. Einstein showed that the total energy E of the moving object is related to its mass and speed.

The velocity of an object relative to an observer plays a central role in special relativity, and to determine this velocity, it is sometimes necessary to add two or more velocities together. We first encountered relative velocity in Projectile Motion Section, so we will begin by reviewing some of the ideas presented there