Until now, we have been concerned mainly with translational motion. Here we will deal with rotational motion. Our understanding of the world around us will be increased significantly—from rotating bicycle wheels and compact discs to amusement park rides, a spinning skater, the rotating Earth, and a centrifuge—and there may be a few surprises.

 

We will consider mainly the rotation of rigid objects about a fixed axis.

 

A rigid object is an object with a definite shape that doesn’t change, so that the particles composing it stay in fixed positions relative to one another (any real object is capable of deforming when a force is exerted on it, but the concept of an ideal rigid object is very useful as a good approximation). The motion of a rigid object can be analyzed as the translational motion of the object’s center of mass, plus rotational motion about its center of mass. We have already discussed translational motion in detail, so now we focus on purely rotational motion. we will develop our understanding of rotational motion in a manner parallel to that used for translational motion in previous articles. We began in past articles by defining kinematic variables for translational motion: position, velocity, and acceleration. We do the same here for rotational motion.

 

By purely rotational motion we mean that all points in the object move in circles, and that the centers of these circles all lie on one line called the axis of rotation.

Every point in an object rotating about a fixed axis moves in a circle whose center is on the axis of rotation and whose radius is $r$, the distance of that point from the axis of rotation. A straight line drawn from the axis to any point in the object sweeps out the same angle $\theta$ in the same time interval.

Angular Position (Polar Coordinate System with O at the axis of rotation)

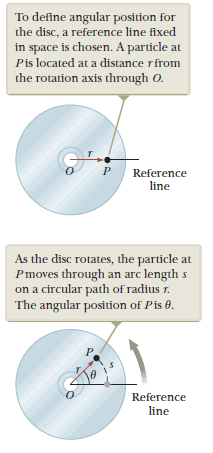To indicate the angular position of a rotating object, or how far it has rotated, we take a small point on the object (moves in a circular path at a fixed distance $r$ from the origin), and specify the angle $\theta$ of a straight line drawn from the axis to small point ($r$) with respect to a reference line, such as the $x$ axis, as shown in the figure:

 

In this representation, the angle $\theta$ changes in time while $r$ remains constant. As the particle moves along the circle from the reference line, which is at angle $\theta=0$, it moves through an arc of length $s$.

 

The angle $\theta$ is often expressed in one of three units. The first is the familiar degree, and it is well known that there are 360 degrees in a circle. The second unit is the revolution (rev), one revolution representing one complete turn of 360°. The most useful unit from a scientific viewpoint, however, is the SI unit called the radian (rad).

The figure shows how the radian is defined, as the disc rotates, the point traces out an arc of length $s$, which is measured along a circle of radius $r$. The angle $\theta$ in radians is defined as:

$$\theta \;\text{(in radians)}=\dfrac{\text{Arc length}}{\text{Radius}}=\dfrac{s}{r} $$

According to this definition, an angle in radians is the ratio of two lengths; for example, meters/ meters. In calculations, therefore, the radian is treated as a number without units and has no effect on other units that it multiplies or divides. Nonetheless when giving an angle in radians (abbreviated rad), we always mention rad to remind us it is not degrees.

One radian is defined as the angle subtended by an arc whose length is equal to the radius.

It is useful to express an angle $\theta$ in radians, because then the arc length $s$ subtended at any radius $r$ can be calculated by multiplying $\theta$ by $r$.

 

To convert between degrees and radians, it is only necessary to remember that the arc length of an entire circle of radius $r$ is the circumference ($2 \pi r$). Therefore, from the above equation, the number of radians that corresponds to one revolution is:

$$\theta =\dfrac{s}{r}=\dfrac{2 \pi r}{r}= 2 \pi \;\mathrm{rad}$$

Since $2 \pi$ rad corresponds to 360°, the number of degrees in one radian is:

$$360^o= 2 \pi \;\mathrm{rad}$$ $$1 \;\mathrm{rad} =\dfrac{360^o}{2 \pi}=57.3^o$$

Because the disc in the above Figure is a rigid object, as the particle moves through an angle $\theta$ from the reference line, every other particle on the object rotates through the same angle $\theta$. Therefore, we can associate the angle $\theta$ with the entire rigid object as well as with an individual particle, which allows us to define the angular position of a rigid object in its rotational motion. We choose a reference line on the object, such as a line connecting $O$ and a chosen particle on the object. The angular position of the rigid object is the angle $\theta$ between this reference line on the object and the fixed reference line in space, which is often chosen as the $x$ axis. Such identification is similar to the way we define the position of an object in one-dimensional translational motion as the distance $x$ between the object and the reference position, which is the origin, $(x = 0)$. Therefore, the angle $\theta$ plays the same role in rotational motion that the position $x$ does in one-dimensional translational motion.

Angular Displacement

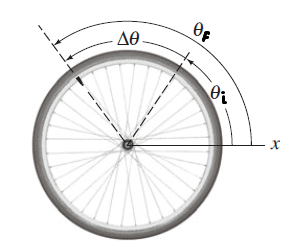When an object such as the bicycle wheel in the Figure rotates from some initial position, specified by $\theta_i$, to some final position, $\theta_f$, the reference line fixed to the object sweeps out an angle $\Delta \theta$, This quantity is defined as the angular displacement of the rigid object:

$$\Delta \theta=\theta_f - \theta_i$$

A rotating object may rotate either counterclockwise or clockwise, the direction can be specified with a + or - sign. And standard convention calls a counterclockwise diisplacement positive and a clockwise displacement negative.

Angular Velocity

The angular velocity, $\omega$, is defined in analogy with linear (translational) velocity. Instead of linear displacement, we use the angular displacement. Thus the average angular velocity of an object rotating about a fixed axis is defined as:

$$\bar{\omega}=\dfrac{\Delta \theta}{\Delta t}$$

where $\Delta \theta$ is the angle through which the object has rotated in the time interval $\Delta t$.

 

The instantaneous angular velocity is the limit of this ratio as $\Delta t$ approaches zero:

$$\omega = \lim_{\Delta t \to 0} \dfrac{\Delta \theta}{\Delta t}$$

Angular velocity is generally specified in radians per second (rad/s), although other units such as revolutions per minute (rev/min or rpm) are also used. Note that all points in a rigid object rotate with the same angular velocity, since every position in the object moves through the same angle in the same time interval.

In agreement with the sign convention adopted for angular displacement, angular velocity is positive when the rotation is counterclockwise and negative when it is clockwise.

Angular velocity may have units of revolutions per minute (rev/min or rpm), because we can relate the angular velocity $\omega$ to the frequency of rotation, $f$. The frequency is the number of complete revolutions (rev) per second. One revolution (of a wheel, say) corresponds to an angle of $2 \pi$ radians, and thus (1 rev/s= $2 \pi$ rad/s). Hence, in general, the frequency $f$ is related to the angular velocity by:

$$f=\dfrac{\omega}{2 \pi} \;\;\;\;\;\;\;\;\;\;\;\;\; \omega=2 \pi f$$

The unit for frequency, revolutions per second (rev s), is given the special name the hertz (Hz). That is, (1 Hz=1 rev/s). Note that “revolution” is not really a unit, so we can also write (1 Hz=1 $s^{-1}$)

The time required for one complete revolution is called the period T, and it is related to the frequency by $T=\dfrac{1}{f}$

Angular Acceleration

Angular acceleration, $\alpha$, in analogy to linear acceleration, is defined as the change in angular velocity divided by the time required to make this change. The average angular acceleration is defined as:

$$\bar{\alpha}=\dfrac{\Delta \omega}{\Delta t}$$

where $\Delta \omega= \omega_f - \omega_i$, $\omega_i$ is the angular velocity initially, and $\omega_f$ is the angular velocity after a time interval $\Delta t$.

 

Instantaneous angular acceleration is defined as the limit of this ratio as approaches $\Delta t$ zero:

$$\alpha = \lim_{\Delta t \to 0} \dfrac{\Delta \omega}{\Delta t}$$

Since $\omega$ is the same for all points of a rotating object, then also $\alpha$ will be the same for all points. Thus, $\omega$ and $\alpha$ are properties of the rotating object as a whole. With $\omega$ measured in radians per second and $t$ in seconds, $\alpha$ has units of radians per second squared ($rad/s^2$). An angular acceleration of $+5 \;rad/s^2$, for example, means that the angular velocity of the rotating object increases by +5 radians per second during each second of acceleration.

Notice that $\alpha$ is positive when a rigid object rotating counterclockwise is speeding up or when a rigid object rotating clockwise is slowing down during some time interval.

Angular position ($\theta$), angular speed ($\omega$), and angular acceleration ($\alpha$) are analogous to translational position ($x$), translational speed ($v$), and translational acceleration ($a$). The variables $\theta$, $\omega$, and $\alpha$ differ dimensionally from the variables $x$, $v$, and $a$ only by a factor having the unit of length.

 

The Vector Nature of Angular Variables

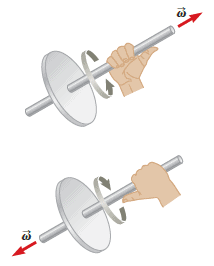Like the linear velocity and the linear acceleration, the angular quantities are also vectors and have a direction as well as a magnitude. We have not specified any direction in space for angular speed and angular acceleration. Because we are considering rotation about a fixed axis, however, we can use nonvector notation and indicate the vectors’ directions by assigning a positive or negative sign to $\omega$ and $\alpha$ as discussed earlier. When a rigid object rotates about a fixed axis, it is the axis that identifies the motion, and the angular velocity vector points along this axis. Therefore, the directions of $\vec{\omega}$ and $\vec{\alpha}$ are along this axis. To illustrate this convention, it is convenient to use the righthand rule demonstrated in the Figure.

Right-Hand Rule: Grasp the axis of rotation with your right hand, so that your fingers circle the axis in the same sense as the rotation. Your extended thumb points along the axis in the direction of the angular velocity vector.

No part of the rotating object moves in the direction of the angular velocity vector.

The direction of $\vec{\alpha}$ follows from its definition. Angular acceleration arises when the angular velocity changes, and the acceleration vector also points along the axis of rotation. The acceleration vector has the same direction as the change in the angular velocity. That is, when the magnitude of the angular velocity (which is the angular speed) is increasing, the angular acceleration vector points in the same direction as the angular velocity. Conversely, when the magnitude of the angular velocity is decreasing, the angular acceleration vector points in the direction opposite to the angular velocity.

In our study of translational motion, after introducing the kinematic variables, we considered the special case of a particle under constant acceleration. We follow the same procedure here for a rigid object under constant angular acceleration.

A complete description of rotational motion requires values for the five variables: angular displacement $\Delta \theta$, the angular acceleration $\alpha$, the final angular velocity $\omega$, the initial angular velocity $\omega_0$, and the elapsed time $\Delta t$.

We summarize these angular equations here, opposite their linear equivalents (for simplicity we choose $\theta_0=0 \;\mathrm{rad}$ at the initial time $t_0=0$):

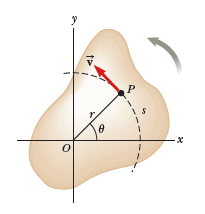Now, we derive some useful relationships between the angular speed and acceleration of a rotating rigid object and the translational speed and acceleration of a point in the object. To do so, we must keep in mind that when a rigid object rotates about a fixed axis, every particle of the object moves in a circle whose center is on the axis of rotation. Let us now generalize to an arbitrary, three-dimensional object, as in Figure:

A reference axis fixed in space is chosen—the x axis in and we look at the motion of one point P contained within the object.

Because point P in moves in a circle, the translational velocity vector $\vec{v}$ is always tangent to the circular path and hence is called tangential velocity.

The magnitude of the tangential velocity of the point P is by definition the tangential speed $v= ds/dt$, where $s$ is the distance traveled by this point measured along the circular path.

Recalling that $s = r \theta$, provided that $\theta$ is measured in radians. and noting that, for a given point on the object, $r$ is constant, we obtain:

$$ v=\dfrac{ds}{dt}=r\dfrac{d \theta}{dt}$$ $$v= r \omega$$

We find the same relationship for particles at every point on a rigid object. Although every point on the rigid object has the same angular speed, not every point has the same tangential speed because $r$ is not the same for all points on the object. this Equation shows that the tangential speed of a point on the rotating object increases as one moves outward from the center of rotation, as we would intuitively expect. For example, the outer end of a swinging golf club moves much faster than a point near the handle.

It is important to emphasize that the angular speed in the above Equation must be expressed in radian measure (e.g., in rad/s); no other units, such as revolutions per second, are acceptable. This restriction arises because the equation was derived by using the definition of radian measure.

We can relate the angular acceleration of the rotating rigid object to the tangential acceleration (the tangential component of the translational acceleration) of the point P. If the time is measured relative to $t_0 = 0$ s, the definition of linear acceleration is given by $\left(a=\dfrac{v-v_0}{t} \right)$, so:

$$a_T=\dfrac{r \omega -r \omega_0}{t}=r \left( \dfrac{ \omega - \omega_0}{t} \right)$$ $$a_T=r \alpha$$

This result shows that, for a given value of $\alpha$, the tangential acceleration $a_T$ is proportional to the radius r. In this expression, the terms $a_T$ and a refer to the magnitudes of the numbers involved, without reference to any algebraic sign. Moreover, as is the case for $\omega$, only radian measure can be used for $\alpha$.

There is an advantage to using the angular velocity $\omega$ and the angular acceleration $\alpha$ to describe the rotational motion of a rigid object. The advantage is that these angular quantities describe the motion of the entire object. In contrast, the tangential quantities $v$ and $a_T$ describe only the motion of a single point on the object, and the above Equations indicate that different points located at different distances $r$ have different tangential velocities and accelerations.

Centripetal Acceleration and Tangential Acceleration

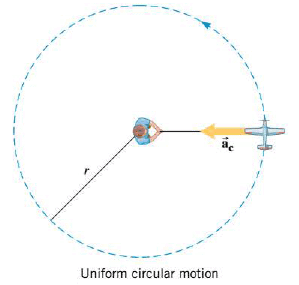When an object picks up speed as it moves around a circle, it has a tangential acceleration, as discussed above. In addition, the object also has a centripetal acceleration, as emphasized in the uniform circuJar motion, in which a particle moves at a constant tangential speed on a circular path. The tangential speed $v$ is the magnitude of the tangential velocity vector. Even when the magnitude of the tangential velocity is constant, an acceleration is present, since the direction of the velocity changes continually. Because the resulting acceleration points toward the center of the circle, it is called the centripetal acceleration. The magnitude of $\vec{a_c}$ is:

$$a_c= \dfrac{v^2}{r}$$

We can express the centripetal acceleration of a particle in uniform circular motion in terms of the object angular speed, $\omega$, by substituting $v$ in the equation for centripetal acceleration:

$$a_c=\dfrac{ \left( r \omega \right)^2}{r}=r \omega^2$$

Only radian measure (rad/s) can be used for win this result, since the relation $v = r \omega$ presumes radian measure.

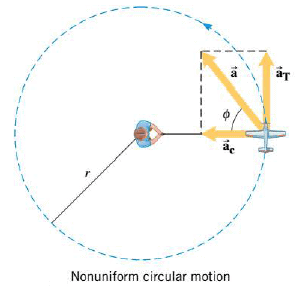While considering uniform circular motion, we ignored the details of how the motion is established in the first place. In the Figure, for instance, assume that the engine of the plane produces a thrust in the tangential direction, and this force leads to a tangential acceleration. In response, the tangential speed of the plane increases from moment to moment, until the situation shown in the drawing results. While the tangential speed is changing, the motion is called nonuniform circular motion.

Since the direction and the magnitude of the tangential velocity are both changing, the airplane experiences two acceleration components simultaneously.

The changing direction means that there is a centripetal acceleration $\vec{a_c}$. The magnitude of $\vec{a_c}$ at any moment can be calculated using the value of the instantaneous angular speed and the radius ($a_c=r \omega^2$).

The fact that the magnitude of the tangential velocity is changing means that there is also a tangential acceleration $\vec{a_T}$. The magnitude of $\vec{a_T}$ can be determined from the angular acceleration a according to $\vec{a_T} = r \alpha$, as we disscused before. The total acceleration is given by the vector sum of $\vec{a_c}$ and $\vec{a_T}$. Since $\vec{a_c}$ and $\vec{a_T}$ are perpendicular, the magnitude of the total acceleration $\vec{a}$ can be obtained from the Pythagorean theorem as:

$$ a = \sqrt{a_c^2 + a_T^2} = \sqrt{r^2 \omega^4 + r^2 \alpha^2}= r \sqrt{ \omega^4 + \alpha^2}$$

and this is the magnitude of the total acceleration at point P on the rotating rigid object.

while the angle $\phi$ in the drawing can be determined from $\left( \tan \phi= a_T / a_c \right)$ .

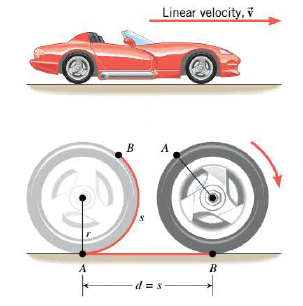The essence of rolling motion is that there is no slipping at the point of contact where the tire touches the ground. To a good approximation, the tires on a normally moving automobile roll and do not slip. In contrast, the squealing tires that accompany the start of a drag race are rotating, but they are not rolling while they rapidly spin and slip against the ground. When the tires in the Figure roll, there is a relationship between the angular speed at which the tires rotate and the linear speed (assumed constant) at which the car moves forward. In the drawing, consider the points labeled A and B on the left tire. Between these points we apply a coat of red paint to the tread of the tire; the length of this circular arc of paint is $s$. The tire then rolls to the right until point B comes in contact with the ground. As the tire rolls, all the paint comes off the tire and sticks to the ground, leaving behind the horizontal red line shown in the drawing. The axle of the wheel moves through a linear distance $d$, which is equal to the length of the horizontal strip of paint. Since the tire does not slip, the distance $d$ must be equal to the circular arc length $s$, measured along the outer edge of the tire:

$$d = s$$

Dividing both sides of this equation by the elapsed time t shows that:

$$\dfrac{d}{t} = \dfrac{s}{t}$$

The term d/t is the speed at which the axle moves parallel to the ground-namely, the linear speed of the car. The term s/t is the tangential speed at which a point on the outer edge of the tire moves relative to the axle (which is related to the angular speed $\omega$ about the axle). Therefore, There is a simple relation between the linear speed $v$ of the axle and the angular velocity of the rotating wheel or sphere: namely, $v = r \omega$ (where r is the radius), and this relationship is valid only if there is no slipping.

 

If the car has a linear acceleration a parallel to the ground, a point on the tire's outer edge experiences a tangential acceleration $a_T$ relative to the axle. The same kind of reasoning as that used in the previous paragraph reveals that the magnitudes of these accelerations are the same and that they are related to the angular acceleration a of the wheel relative to the axle: $a = r \alpha$