The source of any sound is a vibrating object. Almost any object can vibrate and hence be a source of sound. Simple sources of sound are particularly musical instruments (Vibrating Strings and Air Columns). In musical instruments, the source is set into vibration by striking, plucking, bowing, or blowing. Standing waves are produced and the source vibrates at its natural resonant frequencies. The vibrating source is in contact with the air (or other medium) and pushes on it to produce sound waves that travel outward. The frequencies of the waves are the same as those of the source, but the speed and wavelengths can be different. A drum has a stretched membrane that vibrates. Xylophones and marimbas have metal or wood bars that can be set into vibration. Bells, cymbals, and gongs also make use of a vibrating metal. Many instruments make use of vibrating strings, such as the violin, guitar, and piano, or make use of vibrating columns of air, such as the flute, trumpet, and pipe organ. We have already seen that the pitch of a pure sound is determined by the frequency.

When a piano player strikes a piano key, a hammer inside the piano strikes a wire and causes it to vibrate. The wire’s vibrations are then transferred to the piano’s soundboard. As the soundboard vibrates, it exerts a force on air molecules around it, causing the air molecules to move. Because this force is exerted through displacement of the soundboard, the soundboard does work on the air. Thus, as the soundboard vibrates back and forth, its kinetic energy is converted into sound waves. This is one reason that the vibration of the soundboard gradually dies out.

Waves carry energy from one place to another. Energy is given to a water wave, for example, by a rock thrown into the water, or by wind far out at sea. The energy is transported by waves to the shore. The oscillating hand transfers energy to the rope, and that energy is transported down the rope and can be transferred to an object at the other end. All forms of traveling waves transport energy.

The vibrations on the string of a musical instrument, usually consist of many standing waves together at the same time, each of which has a different wavelength and frequency. So the sounds you hear from a stringed instrument, even those that sound like a single pitch, actually consist of multiple frequencies.

Interference is the hallmark of waves, all of which exhibit constructive and destructive interference exactly analogous to that seen for water waves. In fact, one way to prove something “is a wave” is to observe interference effects. So, sound being a wave, we expect it to exhibit interference, such as the beats from two similar notes played simultaneously

Often, two or more sound waves are present at the same place at the same time, as is the case with sound waves when everyone is talking at a party or when music plays from the speakers of a stereo system.

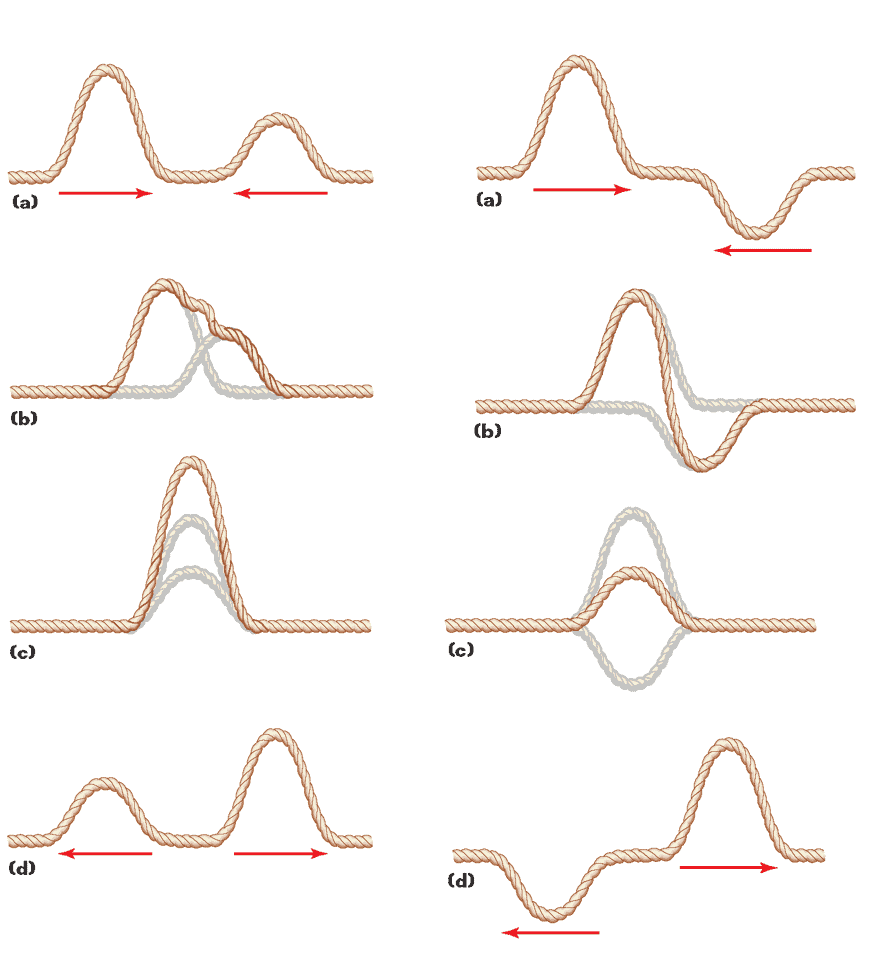
The adding together of individual pulses to form a resultant pulse is an example of a more general concept called the principle of linear superposition:

When two or more waves are present simultaneously at the same place, the resultant disturbance is the sum of the disturbances from the individual waves.

This principle can be applied to all types of waves, including sound waves, water waves, and electromagnetic waves such as light, radio waves, and microwaves. It embodies one of the most important concepts in physics, and the remainder of this article deals with examples related to it.

Constructive and Destructive Interference of Sound Waves

When two waves meet, they interfere constructively if they always meet exactly in phase and destructively if they always meet exactly out of phase. In either case, this means that the wave patterns do not shift relative to one another as time passes. Sources that produce waves in this fashion are called coherent sources.

Beats

We will see in this section that two overlapping waves with slightly different frequencies give rise to the phenomenon of beats. However, the principle of linear superposition again provides an explanation of what happens when the waves overlap.

The principle of linear superposition reveals that overlapping sound waves exhibit interference effects, whereby the sound energy is redistributed within the overlap region. We will now use the principle of linear superposition to explore another interference effect, that of diffraction.

A standing wave is another interference effect that can occur when two waves overlap. Standing waves can arise with transverse waves, such as those on a guitar string, and also with longitudinal sound waves, such as those in a flute. In any case, the principle of linear superposition provides an explanation of the effect, just as it does for diffraction and beats.

Transverse Standing Waves

The series of natural frequencies that lead to standing waves on a string fixed at both ends is:

$$f_n = n \left( \dfrac{v}{2L} \right) \;\;\;\;\;\; n = 1,2,3,4,...$$

Longitudinal Standing Waves

The series of natural frequencies that lead to standing waves on a tube open at both ends is:

$$f_n = n \left( \dfrac{v}{2L} \right) \;\;\;\;\;\; n = 1,2,3,4,...$$

Complex Sound Waves

Musical instruments produce sound in a way that depends on standing waves. sound is produced at the fundamental frequency of the instrument.

In general, however, a musical instrument does not produce just the fundamental frequency when it plays a note, but simultaneously generates a number of harmonics as well. Different instruments, such as a violin and a trumpet, generate harmonics to different extents, and the harmonics give the instruments their characteristic sound qualities or timbres. Suppose, for instance, that a violinist and a trumpet player both sound concert A, a note whose fundamental frequency is 440 Hz. Even though both instruments are playing the same note, most people can distinguish the sound of the violin from that of the trumpet. The instruments sound different because the relative amplitudes of the harmonics (880 Hz, 1320 Hz, etc.) that the instruments create are different.