Uniform Circular Motion

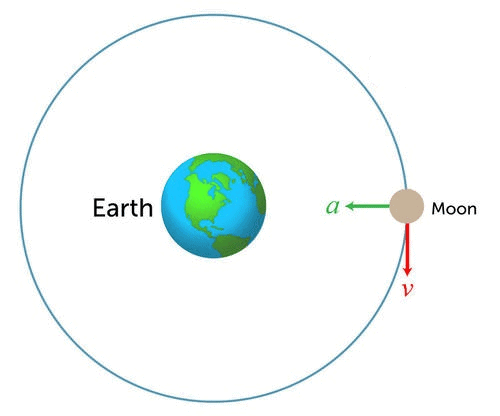
Uniform circular motion is the motion of an object traveling at a constant (uniform) speed on a circular path.

As an example of uniform circular motion consider a stone being whirled on the end of a string or a fixed horse on a merry-go-round. Are these objects accelerating? At first, you might think that they are not because their speeds do not change. However, remember that acceleration is the change in velocity, not just the change in speed. Because their direction is changing, the objects must be accelerating.

Displacement

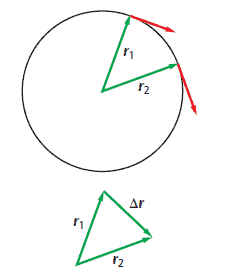
As the object moves around the circle, the position vector length, relative to the center of the circle, does not change, but its direction does.

The object’s displacement over a time interval is the change in position, and can be caluclated by useing a vector diagram where the position vector at the beginning of a time interval $\vec{r_1}$ and the position vector at the end of the time interval $\vec{r_2}$ are subtracted to give the resultant $\vec{\Delta r}$, the displacement during the time interval.

Note: $\left | \vec{r_1} \right |=\left | \vec{r_2} \right |=r$

Speed and velocity

The displacement, $\vec{\Delta r}$, of an object in circular motion, divided by the time interval $\Delta t$ in which the displacement occurs, is the object’s average velocity during that time interval.

$$\bar{\vec{v}}=\dfrac{\vec{\Delta r}}{\Delta t}$$

The velocity vector has the same direction as the displacement, so the constant-magnitude velocity vector is always tangent to the path of the object and perpendicular to the radius of the circular path. Therefore, the direction of the velocity vector is always changing as the object moves around the circle.

Sometimes it is more convenient to describe uniform circular motion by specifying the period of the motion, rather than the speed. The period $T$ is the time required to travel once around the circle- that is, to make one complete revolution. There is a relationship between period and speed if the radius is known, since speed is the distance traveled (here, the circumference of the circle) divided by the time:

$$v=\dfrac{2 \pi r}{T}$$

The definition of uniform circular motion emphasizes that the speed, or the magnitude of the velocity vector, is constant. It is equally significant that the direction of the vector is not constant.

Angular Speed

Because one full revolution of the particle around the circle corresponds to an angle of $2 \pi$ radians, then $2 \pi$ divided by the object period gives the angular speed $\omega$ of the particle (radians/s or $s^{-1}$):

$$\omega=\dfrac{2 \pi}{T}$$

We can find a relationship between angular speed and the translational speed with which the particle travels in the circular path by substituting $T$ in the above equation:

$$\omega=\dfrac{2 \pi}{\left( \dfrac{2 \pi r}{v} \right)}=\dfrac{v}{r}$$ $$v=\omega r$$

this equation demonstrates that, for a fixed angular speed, the translational speed becomes larger as the radial position becomes larger. Therefore, for example, if a merry-go-round rotates at a fixed angular speed $\omega$, a rider at an outer position at large $r$ will be traveling through space faster than a rider at an inner position at smaller $r$. We will investigate this more deeply in Rotational Motion.

Acceleration

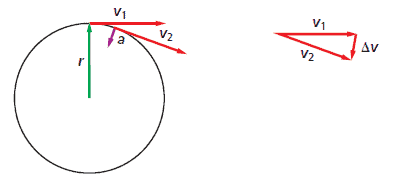Any change in the velocity vector, even if it is only a change in direction, means that an acceleration is occurring. If the velocity vectors $\vec{v_1}$ and $\vec{v_2}$ at the beginning and end of a time interval. The difference in the two vectors, $\vec{\Delta v}$, is found by subtracting the vectors, as shown in the figure:

The change in velocity, $\vec{\Delta v}$, of an object in circular motion, divided by the time interval $\Delta t$ in which the change occurs, is the object’s average acceleration during that time interval:

$$\bar{\vec{a}}=\dfrac{\vec{\Delta v}}{\Delta t}$$

The direction of the change in velocity is toward the center of the circle, and so the acceleration vector also points to the center of the circle. This particular acceleration is called "centripetal acceleration," because it points toward the center of the circle.

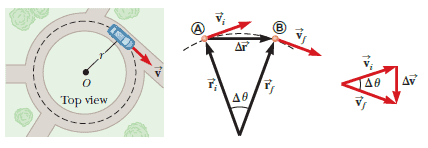
Let us now find the magnitude of the acceleration of the particle. Consider the diagram of the position and velocity vectors in the following Figure:

In the figure, we can identify triangles that help us analyze the motion. The angle $\Delta \theta$ between the two position vectors is the same as the angle between the velocity vectors because the velocity vector $\vec{v}$ is always perpendicular to the position vector $\vec{r}$ . Therefore, the two triangles are similar. (Two triangles are similar if the angle between any two sides is the same for both triangles and if the ratio of the lengths of these sides is the same. $v_i=v_f=v$ and $r_i=r_f=r$) We can now write a relationship between the lengths of the sides for the two triangles in the Figure:

$$\dfrac{\left | \vec{\Delta v} \right |}{v}=\dfrac{\left | \vec{\Delta r} \right |}{r}$$

$$\left | \vec{\Delta v} \right |=\dfrac{v \left | \vec{\Delta r} \right |}{r}$$

this expression can be substituted into average acceleration Equation:

$$\left | \bar{\vec{a}} \right |=\dfrac{\left | \vec{\Delta v} \right |}{\Delta t}= \dfrac{v \left | \vec{\Delta r} \right |}{r \Delta t}$$

Now imagine that points A and B in above Figure become extremely close together. As A and B approach each other, $\Delta t$ approaches zero, $\left | \vec{\Delta r} \right |$ approaches the distance traveled by the particle along the circular path, and the ratio $\dfrac{ \left | \vec{\Delta r} \right |}{ \Delta t}$ approaches the speed $v$. In addition, the average acceleration becomes the instantaneous acceleration at point A. Hence, in the limit $\Delta t \to 0$, the magnitude of the acceleration is:

$$a_c=\dfrac{v^2}{r}$$

An acceleration of this nature is called a centripetal acceleration (centripetal means center-seeking). The subscript on the acceleration symbol reminds us that the acceleration is centripetal.

We can express the centripetal acceleration of a particle in uniform circular motion in terms of the object period, $T$, by substituting $v$ in the equation for centripetal acceleration:

$$a_c=\dfrac{ \left( \dfrac{2 \pi r}{T} \right)^2}{r}=\dfrac{4 \pi^2 r}{T^2}$$

We can express the centripetal acceleration of a particle in uniform circular motion in terms of the object angular speed, $\omega$, by substituting $v$ in the equation for centripetal acceleration:

$$a_c=\dfrac{ \left( r \omega \right)^2}{r}=r \omega^2$$