When you throw a stone into a lake or pool of water, circular waves form and move outward. Waves will also travel along a rope that is stretched out straight on a table if you vibrate one end back and forth. Water waves and waves on a rope or cord are two common examples of mechanical waves, which propagate as oscillations of matter. We will discuss other kinds of waves later, including electromagnetic waves and light.

Waves can move over large distances, but the medium (the water or the rope) itself has only a limited movement, oscillating about an equilibrium point as in simple harmonic motion. Thus, although a wave is not itself matter, the wave pattern can travel in matter. A wave consists of oscillations that move without carrying matter with them.

Waves carry energy from one place to another. Energy is given to a water wave, for example, by a rock thrown into the water, or by wind far out at sea. The energy is transported by waves to the shore. The oscillating hand transfers energy to the rope, and that energy is transported down the rope and can be transferred to an object at the other end. All forms of traveling waves transport energy.

There are two features common to all waves:

1. A wave is a traveling disturbance.

2. A wave carries energy from place to place.

We will consider two basic types of waves, transverse and longitudinal.

Transverse Wave

A transverse wave can be generated using a Slinky, a remarkable toy in the form of a long, loosely coiled spring. If one end of the Slinky is jerked up and down, an upward pulse is sent traveling toward the right. If the end is then jerked down and up, a downward pulse is generated and also moves to the right. If the end is continually moved up and down in simple harmonic motion, an entire wave is produced. The wave consists of a series of alternating upward and downward sections that propagate to the right, disturbing the vertical position of the Slinky in the process.

Transverse wave is one in which the disturbance occurs perpendicular to the direction of travel of the wave. Radio waves, liight waves, and microwaves are transverse waves. Transverse waves also travel on the strings of instruments such as guitars and banjos.

Longitudinal Wave

A longitudinal wave can also be generated with a Slinky. When one end is pushed forward along its length (i.e., longitudinally) and then pulled back to its starting point, a region where the coils are compressed together is sent traveling to the right. If the end is pulled backward and then pushed forward to its starting point, a region where the coils are stretched apart is formed and also moves to the right. If the end is continually moved back and forth in simple harmonic motion, an entire wave is created. The wave consists of a series of alternating compressed and stretched regions that travel to the right and disturb the coils.

Thus, a longitudinal wave is one in which the disturbance occurs parallel to the line of travel of the wave. A sound wave is a longitudinal wave. A water wave is neither transverse nor longitudinal, since the motion of the water particles is not strictly perpendicular or strictly parallel to the line along which the wave travels. Instead, the motion includes both transverse and longitudinal components, since the water particles at the surface move on nearly circular paths.

The Period and Sinusoidal Nature of Waves

A continuous or periodic wave, has as its source a disturbance that is continuous and oscillating. In periodic wave, the repetitive patterns occur as a result of the simple harmonic motion of the left end of the Slinky, so that every segment of the Slinky vibrates in simple harmonic motion. We have discuss the simple harmonic motion of an object on a spring and introduce the concepts of cycle, amplitude, period, and frequency. This same terminology is used to describe periodic waves, such as the sound waves we hear and the light waves we see.

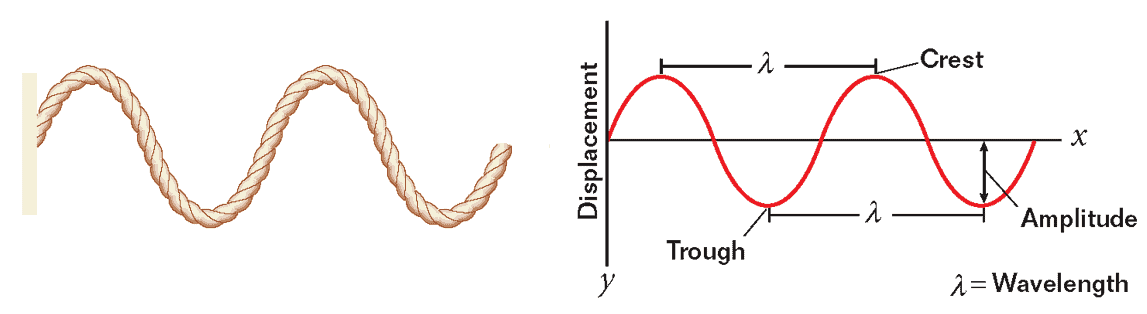
The amplitude A is the maximum excursion of a particle of the medium (i.e., the Slinky) in which the wave exists from the particle's undisturbed position. The amplitude is the distance between a crest, or highest point on the wave pattern, and the undisturbed position; it is also the distance between a trough, or lowest point on the wave pattern, and the undisturbed position. The wavelength $\lambda$ is the horizontal length of one cycle of the wave. The wavelength is also the horizontal distance between two successive crests, two successive troughs, or any two successive equivalent points on the wave.

 

When a wave travels through a medium, it displaces the particles of the medium from their undisturbed positions. Suppose that a particle is located at a distance x from a coordinate origin. We would like to know the displacement y of this particle from its undisturbed position at any time t as the wave passes. For periodic waves that result from simple harmonic motion of the source, the expression for the displacement involves a sine or cosine, a fact that is not surprising. After all, simple harmonic motion is described using sinusoidal equations, and the graphs for a wave look like a plot of displacement versus time for an object oscillating on a spring.

Wave motion toward +x $\;\;\;\;\;\;\;\;\;\; y = A \sin \left( 2 \pi f t - \dfrac{2 \pi x}{\lambda} \right)$

Wave motion toward -x $\;\;\;\;\;\;\;\;\;\; y = A \sin \left( 2 \pi f t + \dfrac{2 \pi x}{\lambda} \right)$

The Speed of Wave

Since the frequency of a wave is f = 1/T, the expression for the speed is:

$$v = \dfrac{\lambda}{T} = \lambda f$$

The fundamental relations f = 1/T and $v = f \lambda$ apply to longitudinal as well as to transverse waves. This shows how the wavelength of a wave is determined by the wave speed and the frequency established by the source.

The following expression for the speed of a small-amplitude wave on a string:

$$v= \sqrt{ \dfrac{F_T}{m/L}}$$

Wave Intensity

The wave intensity I is defined as the wave power P that passes perpendicularly through a surface divided by the area A of that surface:

$$I= \dfrac{P}{A}$$

Sound is a longitudinal wave that is created by a vibrating object, such as a guitar string, the human vocal cords, or the diaphragm of a loudspeaker. Moreover, sound can be created or transmitted only in a n1edium, such as a gas, liquid, or solid. As we will see, the particles of the medium must be present for the disturbance of the wave to move from place to place. Sound cannot exist in a vacuum.

The Speed of Sound

Ideal gas $\;\;\;\;\;\;\;\;\;\; v= \sqrt{ \dfrac{\gamma k T}{m}}$

Liquid $\;\;\;\;\;\;\;\;\;\;\;\; v= \sqrt{ \dfrac{B_{ad}}{\rho}}$

Long, slender, solid bar $\;\;\;\;\;v= \sqrt{ \dfrac{Y}{\rho}}$

Sound Intensity

The sound intensity I is defined as the sound power P that passes perpendicularly through a surface divided by the area A of that surface.

The decibel (dB) is a measurement unit used when comparing two sound intensities. The simplest method of comparison would be to compute the ratio of the intensities. For instance, we could compare $I = 8 \times 10^{-12}$ W/m$^2$ to $I_0 = l \times 10^{-12}$ W/m$^2$ by computing $I/I_0 = 8$ and stating that I is eight times as great as $I_0$. However, because of the way in which the human hearing mechanism responds to intensity, it is more appropriate to use a logarithmic scale for the comparison. For this purpose, the intensity level $\beta$ (expressed in decibels) is defined as follows:

$$ \beta = (10 dB) \log \left( \dfrac{I}{I_0} \right)$$

The Doppler Effect

Have you ever heard an approaching fire truck and noticed the distinct change in the sound of the siren as the truck passes? The effect is similar to what you get when you put together the two syllables "eee" and "yow" to produce "eee-yow." While the truck approaches, the pitch of the siren is relatively high ("eee"), but as the truck passes and moves away, the pitch suddenly drops ("yow"). Something similar, but less familiar, occurs when an observer moves toward or away from a stationary source of sound. Such phenomena were first identified in 1842 by the Austrian physicist Christian Doppler (1803-1853) and are collectively referred to as the Doppler effect.

To explain why the Doppler effect occurs, we will bring together concepts that we have discussed previously-namely, the velocity of an object and the wavelength and frequency of a sound wave. We will combine the effects of the velocities of the source and observer of the sound with the definitions of wavelength and frequency. In so doing, we will see that the Doppler effect is the change in frequency or pitch of the sound detected by an observer because the sound source and the observer have different velocities with respect to the medium of sound propagation.