Many of the terms you have meanings in physics that are similar to their meanings in everyday life. In its everyday sense, the term work means to do something that takes physical or mental effort. But in physics, work has a distinctly different meaning.

 

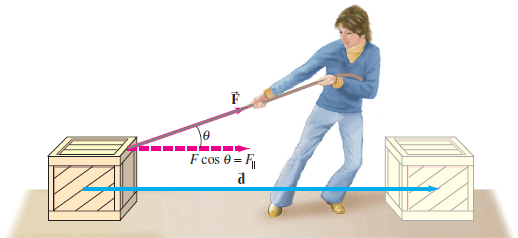
Consider the following situations:

• A student holds a heavy chair at arm’s length for several minutes.

• A student carries a bucket of water along a horizontal path while walking at constant velocity.

It might surprise you to know that as the term work is used in physics, there is no work done on the chair or the bucket, even though effort is required in both cases.

 

The scientific definition of work differs in some ways from its everyday meaning. Certain things we think of as hard work, such as writing an exam or carrying a heavy load on level ground, are not work as defined by a scientist. The scientific definition of work reveals its relationship to energy —whenever work is done, energy is transferred.

For work to be done, a force must be exerted and there must be displacement in the direction of the force. For example, it takes work to push a stalled car. In fact, more work is done when the pushing force is greater or when the displacement of the car is greater. Force and displacement are, in fact, the two essential elements of work

The work $W$ is defined as the magnitude $F$ of the force times the magnitude $s$ of the displacement: $W = Fs$. The work done to push a car is the same whether the car is moved north to south or east to west, provided that the amount of force used and the distance moved are the same. Since work does not convey directional information, it is a scalar quantity. This equation indicates that the unit of work is the unit of force times the unit of distance, or the newton.meter in SI units. One newton.meter is referred to as a joule (J), in honor of James Joule (1818-1889) and his research into the nature of work, energy, and heat.

Work Done by a Constant Force

Formally, the work done on a system by a constant force is defined to be the product of the component of the force in the direction of motion times the distance through which the force acts.

Often, the force and displacement do not point in the same direction. For instance, a suitcase-on-wheels being pulled to the right by a force that is applied along the handle. The force is directed at an angle $\theta$ relative to the displacement. In such a case, only the component of the force along the displacement is used in defining work, this component is $F \cos \theta$, and the general definition of work is:

$$W= (F \cos \theta) s$$

When the force points in the same direction as the displacement, then $\theta = 0$°, and the above Equation reduces to $W = Fs$.

The definition of work takes into account only the component of the force in the direction of the displacement. The force component perpendicular to the displacement does no work. To do work, there must be a force and a displacement, and since there is no displacement in the perpendicular direction, there is no work done by the perpendicular component of the force. If the entire force is perpendicular to the displacement, the angle $\theta$ is 90°, and the force does no work at all.

Work can be either positive or negative, depending on whether a component of the force points in the same direction as the displacement or in the opposite direction. Here is some examples of work:

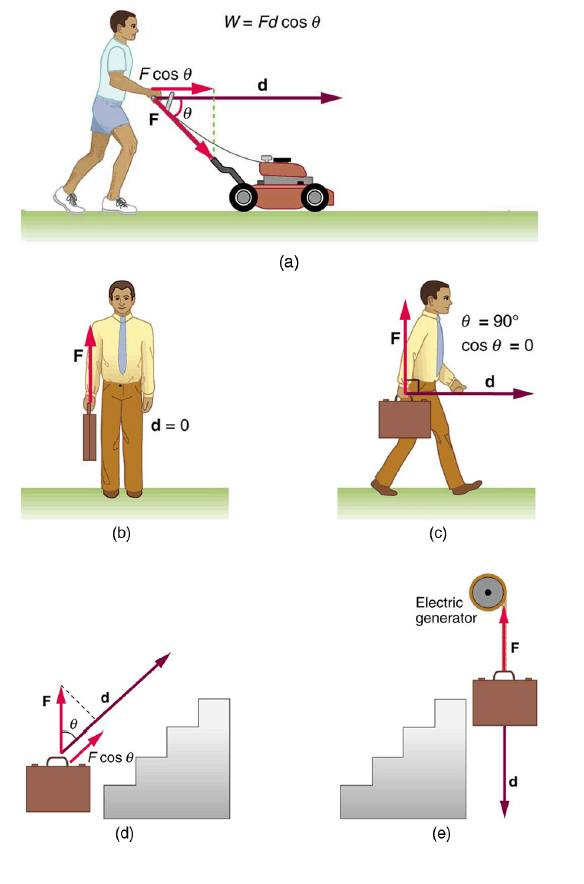
In the above figure, The person holding the briefcase in (b) does no work, Here d = 0 , so W = 0 . Why is it you get tired just holding a load? The answer is that your muscles are doing work against one another, but they are doing no work on the system of interest (the “briefcase-Earth system”). There must be displacement for work to be done, and there must be a component of the force in the direction of the motion. For example, the person carrying the briefcase on level ground in (c) does no work on it, because the force is perpendicular to the motion. That is, $\cos 90$° = 0 , and so W = 0 .

In contrast, when a force exerted on the system has a component in the direction of motion, such as in (d), work is done. energy is transferred to the briefcase. Finally, in (e), energy is transferred from the briefcase to a generator. There are two good ways to interpret this energy transfer. One interpretation is that the briefcase's weight does work on the generator, giving it energy. The other interpretation is that the generator does negative work on the briefcase, thus removing energy from it. The drawing shows the latter, with the force from the generator upward on the briefcase, and the displacement downward. This makes $\theta$ = 180° , and $\cos 180 = -1$ ; therefore, W is negative.

What happens to the work done on a system? Energy is transferred into the system, but in what form? Does it remain in the system or move on? The answers depend on the situation. For example, if the lawn mower in the above Figure (a) is pushed just hard enough to keep it going at a constant speed, then energy put into the mower by the person is removed continuously by friction, and eventually leaves the system in the form of heat transfer. In contrast, work done on the briefcase by the person carrying it up stairs in the above Figure (d) is stored in the briefcase-Earth system and can be recovered at any time, as shown in Figure (e). In fact, the building of the pyramids in ancient Egypt is an example of storing energy in a system by doing work on the system. Some of the energy imparted to the stone blocks in lifting them during construction of the pyramids remains in the stone-Earth system and has the potential to do work.

Work Done by a Variable Force

The work W done by a constant force (constant in both magnitude and direction) is given as $W = (F \cos \theta)s$. Quite often, situations arise in which the force is not constant but changes with the displacement of the object.

When the force varies with the displacement, we cannot use the relation $W = (F \cos \theta)s$ to find the work, because this equation is valid only when the force is constant. However, we can use a graphical method. In this method we divide the total displacement into very small segments, $\Delta s_1$, $\Delta s_2$, and so on. For each segment, the average value of the force component is indicated by a short horizontal line.

Energy is one of the most important concepts in science. Yet we cannot give a simple general definition of energy in only a few words. Nonetheless, each specific type of energy can be defined fairly simply. In this article we define translational kinetic energy and some types of potential energy. Later, we will examine other types of energy, such as that related to heat and electricity. The crucial aspect of energy is that the sum of all types, the total energy, is the same after any process as it was before: that is, energy is a conserved quantity.

For the purposes of this article, we can define energy in the traditional way as “the ability to do work.” This simple definition is not always applicable, but it is valid for mechanical energy which we discuss in this article. We now define and discuss various types of work and forms of energy.

Kinetic Energy (energy of motion) and the Work-Energy Theorem

Some types of work done by the net force gives a system energy of motion (making it move), A moving object can do work on another object it strikes. A flying cannonball does work on a brick wall it knocks down; a moving hammer does work on a nail it drives into wood. In either case, a moving object exerts a force on a second object which undergoes a displacement. An object in motion has the ability to do work and thus can be said to have energy. The energy of motion is called kinetic energy, from the Greek word kinetikos, meaning “motion.”

To obtain a quantitative definition for kinetic energy, let us consider a simple rigid object of mass m (treated as a particle) that is moving in a straight line with an initial speed $v_i$. To accelerate it uniformly to a speed $v_f$ a constant net force $F$ is exerted on it parallel to its motion over a displacement $s$. Then the net work done on the object is: $W =F s$

The relationship that relates work to the change in kinetic energy is known as the work-energy theorem. This theorem is obtained by bringing together three basic concepts that we've already learned about. First, we'll apply Newton's second law of motion, $\sum F = ma$, which relates the net force to the acceleration a of an object. Then, we'll determine the work done by the net force when the object moves through a certain distance. Finally, we'll use one of the equations of kinematics, to relate the distance and acceleration to the initial and final speeds of the object. The result of this approach will be the work-energy theorem.

According to the work-energy theorem, a moving object has kinetic energy, because work was done to accelerate the object from rest to a speed. Conversely, an object with kinetic energy can perform work, if it is allowed to push or pull on another object.

Potential Energy

A system may also have potential energy, which is the energy associated with forces that depend on the position or configuration of an object (or objects) relative to the surroundings. Various types of potential energy (PE) can be defined, and each type is associated with a particular force. The concept of potential energy is associated only with a type of force known as a "conservative" force, as we will discuss. Perhaps the most common example of potential energy is gravitational potential energy.

Gravitational Potential Energy (Work Done by or against the Force of Gravity)

A heavy brick held high above the ground has potential energy because of its position relative to the Earth. The raised brick has the ability to do work, for if it is released, it will fall to the ground due to the gravitational force, and can do work on, say, a stake, driving it into the ground.

Work Done By Gravity: a basketball of mass m moving vertically downward, the force of gravity $mg$ being the only force acting on the ball. The initial height of the ball is $h_0$, and the final height is $h_f$, both distances measured above some reference level. To calculate the work W gravity done on the balll by the force of gravity, we use $W = (F \cos \theta)s$ with $F = mg$ and $\theta = 0$°, since the force and displacement are in the same direction: $W_{gravity}= mg (h_f - h_0)$

Only the difference $(h_f - h_0)$ appears in the above Equation, so $h_0$ and $h_f$ themselves need not be measured from the earth. For instance, they could be measured relative to a level that is one meter above the ground, and the difference $(h_f - h_0)$ would still have the same value. The gravitational potential energy of a book held high above a table, for example, does not depends on whether we measure the height from the top of the table, from the floor, or from some other reference point. What is physically important in any situation is the change $(h_f - h_0)$, because that is what is related to the work done.

 

Work Done Against Gravity: For an object of mass m to be lifted vertically, an upward force must be exerted on it, say by a person’s hand. To lift the object without acceleration, the force needed to lift it is equal to its weight $mg$. So, the person does work equal to: $W_{person}= (mg \cos 0)(h_f - h_0) = mg (h_f - h_0)$, This work done on the object is put into (or gained by) the object (recognizing that this is energy stored in the gravitational field of Earth). Gravity is also acting on the object as it moves and does work on the object equal to: $W_{gravity}= (mg \cos 180)(h_f - h_0) = - mg (h_f - h_0)$. Potential energy is a property of a system rather than of a single object—due to its physical position. An object’s gravitational potential is due to its position relative to the surroundings within the Earth-object system. The force applied to the object is an external force, from outside the system.

Then, the gravitational potential energy $PE_G$ is the energy that an object of mass m has by virtue of its position relative to the surface of the earth. That position is measured by the height of the object relative to an arbitrary zero level. We therefore define the gravitational potential energy of an object as the product of the object’s weight and its height above some reference level (such as the ground):

$$PE_G = mgh$$

The higher an object is above the ground, the more gravitational potential energy it has, and the work done by a net external force to move the object from position 1 to position 2 without acceleration is:

$$W_{person}= mg (h_f - h_0)= PE_f - PE_0= \Delta PE_G$$

Equivalently, we can define the change in gravitational potential energy, in terms of the work done by gravity itself:

$$W_{gravity}= - mg (h_f - h_0)= - \Delta PE_G$$

That is, the change in gravitational potential energy as the object moves from position 1 to position 2 is equal to the negative of the work done by gravity itself.

 

The gravitational potential energy is valid for any path taken between the initial and final heights, and not just for the straight-down path. Thus, only the difference in vertical distances $(h_f - h_0)$ need be considered when calculating the work done by gravity. An important result concerns the gravity force, which does work only in the vertical direction: the work done by gravity depends only on the vertical height, and not on the path taken, whether it be purely vertical motion or, say, motion along an incline. We are assuming here that the difference in heights is small compared to the radius of the earth, so that the magnitude of the acceleration due to gravity $g$ is the same at every height. Moreover, for positions close to the earth's surface, we can use the value of $g = 9.8 \;\; m/s^2$.

Potential Energy of Elastic Spring

We now consider potential energy associated with elastic materials, which includes a great variety of practical applications.

A spring also has potential energy when the spring is stretched or compressed, which we refer to as elastic potential energy. Because of elastic potential energy, a stretched or compressed spring can do work on an object that is attached to the spring.

 

The elastic potential energy $PE_{elastic}$ is the energy that a spring has by virtue of being stretched or compressed. For an ideal spring that has a spring constant k and is stretched or compressed by an amount x relative to its unstrained length, the elastic potential energy is:

$$PE_{elastic} = \dfrac{1}{2} k x^2$$

Conservative Versus Nonconservative Forces

The gravitational force has an interesting property that when an object is moved from one place to another, the work done by the gravitational force does not depend on the choice of path. the work done by gravity depends only on the initial and final heights, and not on the path between these heights. For this reason, the gravitational force is called a conservative force, according to the definition of a CONSERVATIVE FORCE:

A force is conservative when the work it does on a moving object is independent of the path between the object's initial and final positions.

OR A force is conservative when it does no net work on an object moving around a closed path, starting and finishing at the same point.

The gravitational force is our first example of a conservative force. Later, we will encounter others, such as the elastic force of a spring and the electrical force of electrically charged particles. With each conservative force we will associate a potential energy, as we have already done in the gravitational case. The concept of potential energy is not defined for a nonconservative force.

Work-Energy Extended: Converting Between Potential Energy and Kinetic Energy

Gravitational potential energy may be converted to other forms of energy, such as kinetic energy. If we release the mass, gravitational force will do an amount of work equal to mgh on it, thereby increasing its kinetic energy by that same amount.

We can extend the work-energy principle to include potential energy. Suppose several forces act on an object which can undergo translational motion. And suppose conservative forces (such as gravity) and nonconservative forces (such as friction and air resistance) act simultaneously on the object. We write the total (net) work as a sum of the work done by conservative forces, and the work done by nonconservative forces:

$$W_{net}= W_C + W_{NC}$$

Then, from the work-energy principle $W_{net}=\Delta KE$, we have:

$$W_C + W_{NC} =\Delta KE$$ $$W_{NC}= \Delta KE - W_C$$

Work done by a conservative force can be written in terms of potential energy, as we saw for gravitational potential energy $W_{gravity}= - \Delta PE_G$:

$$W_{NC}= \Delta KE + \Delta PE$$

Thus, the work done by all the nonconservative forces acting on an object is equal to the total change in kinetic and potential energies.

In many situations, the time it takes to do work is just as important as the amount of work that is done. Consider two automobiles that are identical in all respects (e.g., both have the same mass), except that one has a "souped-up" engine. The car with the souped-up engine can go from O to 27 m/s (60 mph) in 4 seconds, while the other car requires 8 seconds to achieve the same speed. Each engine does work in accelerating its car, but one does it more quickly. Where cars are concerned, we associate the quicker performance with an engine that has a larger horsepower rating. A large horsepower rating means that the engine can do a large amount of work in a short time. In physics, the horsepower rating is just one way to measure an engine's ability to generate power. The idea of power incorporates both the concepts of work and time, for power is work done per unit time.

Everyone uses machines every day. Some are simple tools, such as bottle openers and screwdrivers, while others are complex, such as bicycles and automobiles. Machines, whether powered by engines or people, make tasks easier. A machine eases the load by changing either the magnitude or the direction of a force to match the force to the capability of the machine or the person.

Consider the bottle opener. When you use the opener, you lift the handle, thereby doing work on the opener. The opener lifts the cap, doing work on it. The work that you do is called the input work, $W_i$. The work that the machine does is called the output work, $W_o$. Recall that work is the transfer of energy by mechanical means. You put work into a machine, such as the bottle opener. That is, you transfer energy to the opener. The opener, in turn, does work on the cap, thereby transferring energy to it. The opener is not a source of energy, and therefore, the cap cannot receive more energy than the amount of energy that you put into the opener. Thus, the output work can never be greater than the input work. The machine simply aids in the transfer of energy from you to the bottle cap.

The force exerted by a person on a machine is called the effort force, $F_e$. The force exerted by the machine is called the resistance force, $F_r$. So in the bottle opener, $F_e$ is the upward force exerted by the person using the bottle opener and $F_r$ is the upward force exerted by the bottle opener. The ratio of resistance force to effort force, Fr/Fe, is called the mechanical advantage, MA, of the machine.